Data
- Title: \(\mathfrak{sl}_3\)-web bases, intermediate crystal bases and categorification
- Author: Daniel Tubbenhauer
- Status: J. Algebraic Combin. 40-4 (2014), 1001-1076. Last update: Wed, 5 Mar 2014 10:57:55 GMT
- ArXiv link: http://arxiv.org/abs/1310.2779
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1, Slides2
Abstract
We give an explicit graded cellular basis of the \(\mathfrak{sl}_3\)-web
algebra \(K_S\).
In order to do this, we identify Kuperberg's basis for the \(\mathfrak{sl}_3\)-web
space \(W_S\) with a version of Leclerc-Toffin's intermediate crystal basis and we
identify Brundan, Kleshchev and Wang's degree of tableaux with the weight of flows on webs and the \(q\)-degree of foams.
We use this to give a “foamy” version of Hu and Mathas graded cellular basis of the cyclotomic Hecke
algebra which turns out to be a graded cellular basis of the \(\mathfrak{sl}_3\)-web algebra \(K_S\).
We restrict ourselves to the \(\mathfrak{sl}_3\) case here, but our approach should,
up to the combinatorics of \(\mathfrak{sl}_n\)-webs, work for all \(n>1\).
A few extra words
In the case of the \(\mathfrak{sl}_2\) analogon of the \(\mathfrak{sl}_3\)-web
algebra \(K_S\) a lot of basic representation theoretic questions are way easier to prove (but usualy still non-trivial).
A good example is the explicit construction of a graded cellular basis - something Brundan and Stroppel did in a nice and
purely combinatorial fashion in the \(\mathfrak{sl}_2\) case (see here).
It turns out that one of the main problems in the \(\mathfrak{sl}_3\) case (getting worse for
bigger \(n\)) is that the dual canonical basis of the underlying web
space is NOT the usual web basis. In fact, we show that Kuperberg's web basis is still special by identifying it with an intermediate crystal basis.
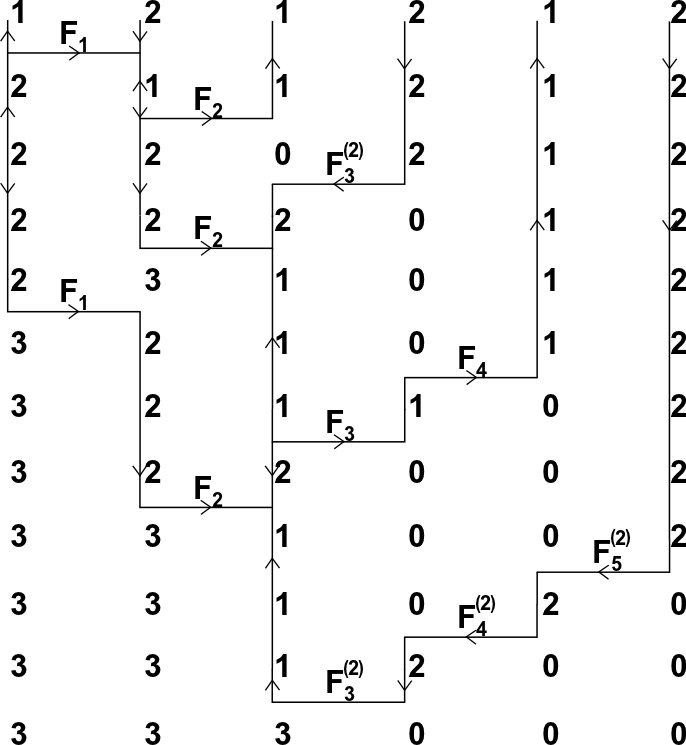
There is an algorithm to compute the intermediate crystal basis. This can be transferred (using quantum skew Howe duality)
to the \(\mathfrak{sl}_3\)-web framework. An example is illustrated below, i.e.
each web gives rise to a string of \(F\) operators that generate the web from a highest weight vector.
We have categorified this algorithm by giving an algorithm to produce foams that form an explicit cellular basis.