A picture is worth a thousand words
My research is e.g. about this (click to enlarge):
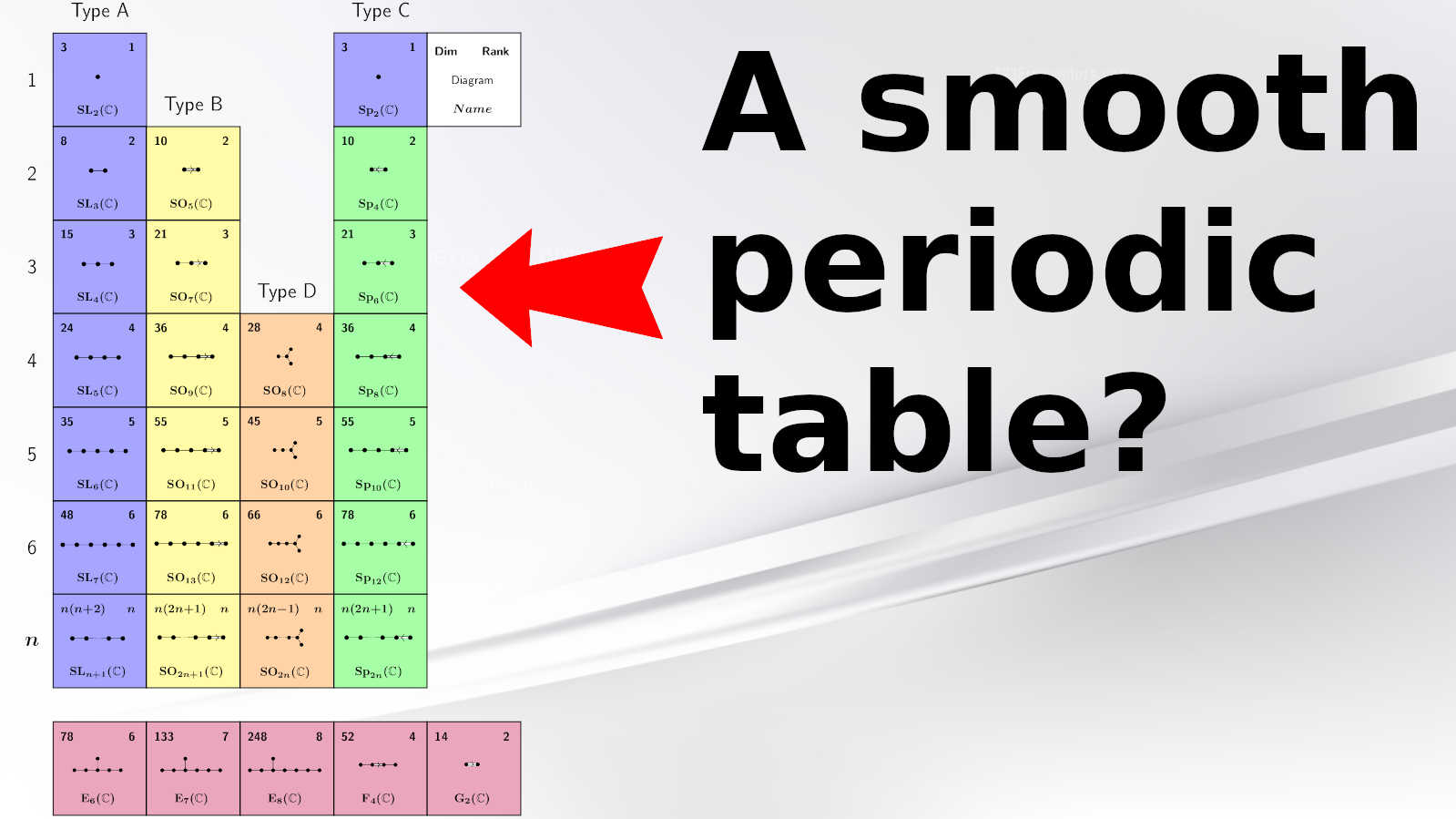
Ok, let me give some more details. A formula is worth a thousand pictures:
- Research statement (quite recent): available here.
- Research statements (not up to date and quite old): available here, here, here, here, here, here, and here.
- Higher representation theory.
- Higher category theory (especially for \(n=2\)) and categorification.
- Applications in low dimensional topology (e.g. knot theory link polynomials and homologies etc.).
- Applications in the representation theory of Lie algebras, quantum groups, diagram algebras and finite-dimensional algebras.
- Some talks of mine for a more general (mathematical) audience: Talk1, Talk2, Talk3, Talk4, Talk5, Talk6, Talk7, Talk8, Talk9, Talk10
For laypersons
Symmetry is everywhere, and nature is designed symmetrically: Snails make their shells, spiders design their webs, and bees build hexagonal honeycombs, all based on the concept of symmetry. Indeed, symmetry is a general principle, which plays an important role in various areas of knowledge and perception, ranging from arts and aesthetics to natural sciences and mathematics. It is a commonplace - though a vitally important commonplace - that symmetry plays a crucial role in our apprehension of pattern, and that it is central to our comprehension of the real world. There is no need to stress the importance of symmetry in geometry, or more generally, in mathematics, but the concept of symmetry goes beyond the borders of these fields as famously captured by the phrase "Beauty is truth". For example, nature has not designed a butterfly to suit our eyes (it certainly does), but rather based on physical and geometric optimization principals which are almost always connected to symmetry. Not surprisingly, studying symmetry systematically is of fundamental importance for understanding the world around us. However, it is also very hard to understand it in this generality. But first hings first, how to define the notion symmetry to begin with?Geometrically, symmetry means that one shape becomes exactly like another when you move it in some way, e.g. turn, flip or slide. Examples are ball-and-stick models of molecules. These naturally exhibit the symmetry properties of macroscopic objects: they pass into congruent forms upon application of bodily rotations about proper and improper axes of symmetry.
Most relevant for me is Felix Klein's view on symmetry. With every geometry and every geometric object, Felix Klein associated an underlying so-called group of symmetries, and this group acts on the geometric objects by transformations such as rotation. More generally, mathematically symmetry is a type of invariance: the property that something does not change under a set of transformations, with the transformations forming a group which acts on the spaces or objects in question.
Not surprisingly, the study of group actions is of paramount importance in mathematics and related field, and, as mentioned above, can be seen as the mathematical study of symmetries. There are numerous examples and applications of group actions in many branches of mathematics, including algebra, topology, geometry, number theory, and analysis, as well as the sciences, including chemistry and physics. For chemistry, as mentioned above, symmetries of molecules and the action of the corresponding group of symmetries play an important role, while in e.g. quantum mechanics, bosons have representatives that are symmetric under permutation operators, and fermions have antisymmetric representatives, and they can be distinguished using group actions.
The linear shadow of the study of group actions is called representation theory, as pioneered by Frobenius and Burnside at the beginning of the 20th century. Nowadays representation theory has many applications within mathematics, but also beyond as e.g. in physics or chemistry. The main idea is that representation theory is a linear shadow of symmetry itself - like a tangent to a curve - and it captures the most important features of the concept in an accessible way. It should come as no surprise that representation theory is one of the most useful incarnations of modern mathematics - within the field, but also e.g. in molecular chemistry. For example, the difference between saturated and unsaturated fat mostly comes from how these molecules arrange themselves in space - which can be studied using representation theory.
My research starts where representation theory started 120 years ago, namely mostly with the abstract theory of what one could call "the representation theory of the 21th century" - the modern way of studying symmetries and my main research area. Under the slogan of 2-representations my research aims to advance a study of the hidden structures beyond the tangent, and with no doubt this way of studying symmetry will have profound applications in 120 years from now, but most likely already much earlier. The classical example are groundbreaking works of Chuang-Rouquier and Khovanov-Lauda on categorifications of quantum groups and their representations, which on the one hand opened a completely new field of research, and on the other hand solved longstanding open problems in other fields.
In other words, my research topic is within abstract areas of mathematics, more precisely representation and category theory, as well as algebra and homological algebra. The main idea is to study the action of monoidal categories or 2-categories on categorical analogs of vector spaces, which can be seen as a categorification of the classical study of an algebra acting on a vector space. The field systematically studying such actions is called 2-representation theory.
