Data
- Title: Two-color Soergel calculus and simple transitive 2-representations
- Authors: Marco Mackaay and Daniel Tubbenhauer
- Status: Canad. J. Math. 71 (2019), no. 6, 1523-1566. Last update: Mon, 23 Apr 2018 14:56:01 GMT
- ArXiv link: https://arxiv.org/abs/1609.00962
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1, Slides2, Slides3, Slides4, Slides5, Slides6, Slides7, Slides8
Abstract
In this paper we complete the \(\mathrm{ADE}\)-like
classification
of simple transitive 2-representations
of Soergel bimodules
in finite dihedral type, under the assumption of gradeability. In particular, we use bipartite
graphs and zigzag algebras of \(\mathrm{ADE}\) type to give an explicit construction of a graded (non-strict)
version of all these 2-representations.
Moreover,
we give simple combinatorial
criteria for when two such 2-representations are
equivalent and for when their Grothendieck groups
give rise to isomorphic representations.
Finally, our construction
also gives a large class of simple transitive 2-representations
in infinite dihedral type for general bipartite graphs.
A few extra words
An essential problem in classical representation
theory is the classification of the simple representations
of any given algebra, i.e. the parametrization of their
isomorphism classes and the explicit construction of a
representative of each class.
Basically the same question arises in 2-representation theory, where the actions of algebras on
vector spaces are replaced by functorial actions of
2-categories on certain 2-categories.
Examples are 2-representations of the 2-categories which categorify
representations of quantum groups, due to (Chuang-)Rouquier
and Khovanov-Lauda, and 2-representations of the 2-category
of Soergel bimodules, which categorify representations of Hecke algebras.
An appropriate
categorical analogue of the simple representations
of finite-dimensional algebras are the so-called
simple transitive 2-representations (of
finitary 2-categories). The problem
of their classification is very hard in general and not well
understood.
In this paper, we construct all (graded) simple transitive 2-representations
(of the small quotient) of the Soergel bimodules of dihedral type (including the infinite dihedral type)
by using
the so-called two-color Soergel calculus.
Our construction is completely explicit
and emphasizes the usage of bipartite graphs which we use to cook up algebras and the 2-categories of
their projective endofunctors, on which the two-color Soergel calculus acts.
The main results are then that we can show that
two simple transitive 2-representations are equivalent
if and only if the corresponding bipartite graphs are
isomorphic (as bipartite graphs), and all such 2-representations arise in this way.
Finally,
we also determine when simple transitive 2-representations
decategorify to isomorphic representations of the corresponding Hecke
algebra, using a purely graph-theoretic property.
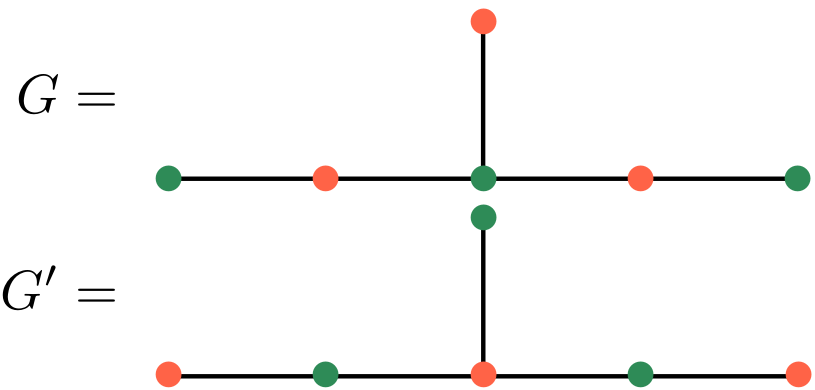
Hereby we obtain
examples of inequivalent
simple transitive 2-representations of the
same 2-category which decategorify
to isomorphic representations, e.g.: