Data
- Title: Functoriality of colored link homologies
- Authors: Michael Ehrig, Daniel Tubbenhauer and Paul Wedrich
- Status: Proc. Lond. Math. Soc. (3) 117 (2018), no. 5, 996-1040. Last update: Fri, 15 Jun 2018 06:18:33 GMT
- ArXiv link: https://arxiv.org/abs/1703.06691
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1, Slides2
Abstract
We prove that the bigraded colored Khovanov-Rozansky type A link and tangle invariants are functorial with respect to link and tangle cobordisms.
A few extra words
Khovanov-Rozansky introduced a
link homology theory categorifying the
type A Reshetikhin-Turaev
invariant. Their homology theory associates
bigraded vector spaces
to link diagrams, two of which are isomorphic whenever the diagrams
differ only by Reidemeister moves.
One of the main advantages of classical homology vs. Betti numbers
for topological spaces is that the former
is a functor. That is, homology “knows” about
“relations” between topological spaces.
Hence, it makes sense to ask the very same question for
Khovanov-Rozansky's invariant and their (exterior) colored
“friends”.
The goal of this paper is to answer
this affirmatively, i.e. to prove
the functoriality of Khovanov-Rozansky link homologies for \(N\geq 2\) under link cobordisms.
In fact, we prove the general functoriality statement in a
framework that is different to and more general than Khovanov-Rozansky's
construction. Namely, by using certain foam categories (canopolises)
which e.g. enables us to immediately prove functoriality for
tangles rather than links.
Moreover, a key idea for our paper (which goes
back to Bar-Natan) is the
insight that the canopolis framework allows a low-effort proof
of the fact that Khovanov-Rozansky link homologies are
functorial up to scalars. This amounts to a significant proof shortcut, as it then only remains to
ensure that these scalars are equal to one. However, this is still a formidable challenge.
To overcome this:
Another key idea for our paper is
Blanchet's use of a Lee-type deformation
for proving the functoriality of a modified
version of Khovanov homology. He
first proved functoriality up to scalars along Bar-Natan's
strategy and then computed these
scalars, and showed them to be equal to one, by working in
the much simpler setting of the deformation. We basically
do the same for the colored Khovanov-Rozansky
invariants.
One advantage of this is that the
undeformed, colored link invariant, as well as all its deformations, can be
obtained as specializations of a unifying equivariant theory.
We then prove that the equivariant theory is functorial up to scalars
and that all its specializations inherit this property with the same scalars.
It then only remains to compute these scalars in the Lee-type deformation, which is significantly simpler.
In particular, we only need to check scalars for so-called
simple resolutions for which we can nail down them explicitly.
Here is
an example of what one needs to prove for the
(in)famous tetrahedron move MM10:
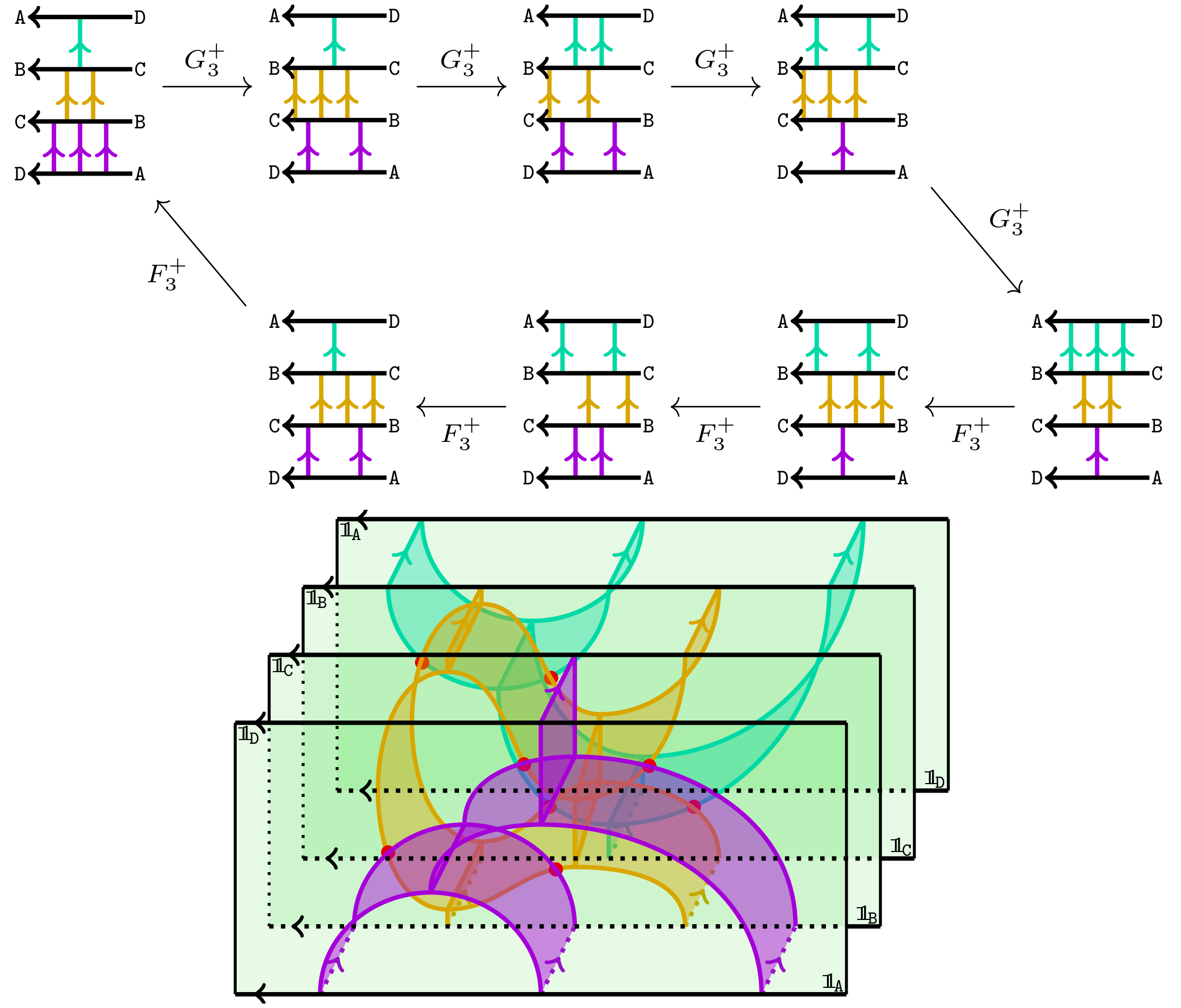
In the uncolored case all “in between edges and facets” in the picture above vanish and the whole prove of checking MM10 boils down to observe that the identity foam is the identity foam.
In fact, this is not a coincidence: using our approach almost no calculations need to be done in the uncolored case.
