The category number

A common joke is that everyone has a minimal number \(n\in\mathbb{N}\) such that, if someone mentions an n-category, one stops thinking. My personal number is maybe \(n=2\): afterward my pet example “n-dimensional cobordisms embedded into an n+1-dimensional-space” (see below) gets quite hard to imagine (left aside the problem to draw these cobordisms).
Let me give now some more details.

Let me be a bit sloppy

I must admit that I tend to be quite sloppy with the notation of an n-category. To be more precise, I should write \((n,n)\)-category instead of n-category, i.e. I never assume that higher morphisms are invertible.
But I am even sloppier sometimes, i.e. if I speak of an n-category I tend to ignore the difference between a weak and a strict n-category. Note that in case \(n\leq 2\) this can be (sometimes) justified by a corresponding coherence theorem.
I am also very sloppy when it comes to more fundamental set theoretical and logical questions, e.g. the subtleties one needs to define the “categories of categories” and related concepts.
Much more details, e.g. a discussion of weak and strict n-categories, can be, for example, found in Leinster's book here.

A rough description

The idea behind higher category theory is easy to explain. It is a generalization of category theory, which can be seen as generalization of set theory.
The slogan for me is that a category is a collection of “set like structures” with the category of sets as a blueprint example. A 2-category is a collection of “category like structures” with the 2-category of categories as a blueprint example. A 3-category is a collection of “2-category like structures”...
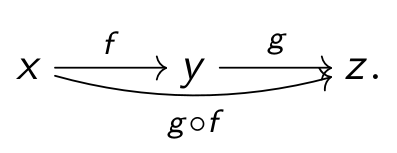
Imagine a set as a collection of points (aka \(0\)-cells), then a 1-category, also know as category, is a one-dimensional structure connecting the objects with some one-dimensional cells called morphisms. The usual notation for this is

Note that the morphisms come with an extra structure, i.e. they can be composed as The composition should satisfy some standard axioms. The idea of higher categories is to “add new structure, i.e. higher arrows between arrows”.
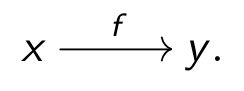
For example, if one starts with a usual category, then one can add two-dimensional cells between the one-dimensional cells and one gets a picture like These new arrows can be composed in two ways called vertical and horizontal. This gives a 2-category a topological structure. Note that the horizontal composition is a 2-cell from \(h\circ f\) to \(j\circ g\) (both composition arrows are not pictured). The composition should satisfy some standard axioms again. If one continues in this fashion, i.e. adding n-cells with n ways of composition, and if one adds some axioms, then one gets a n-category.
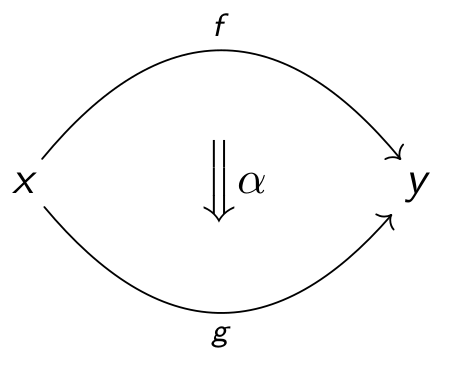
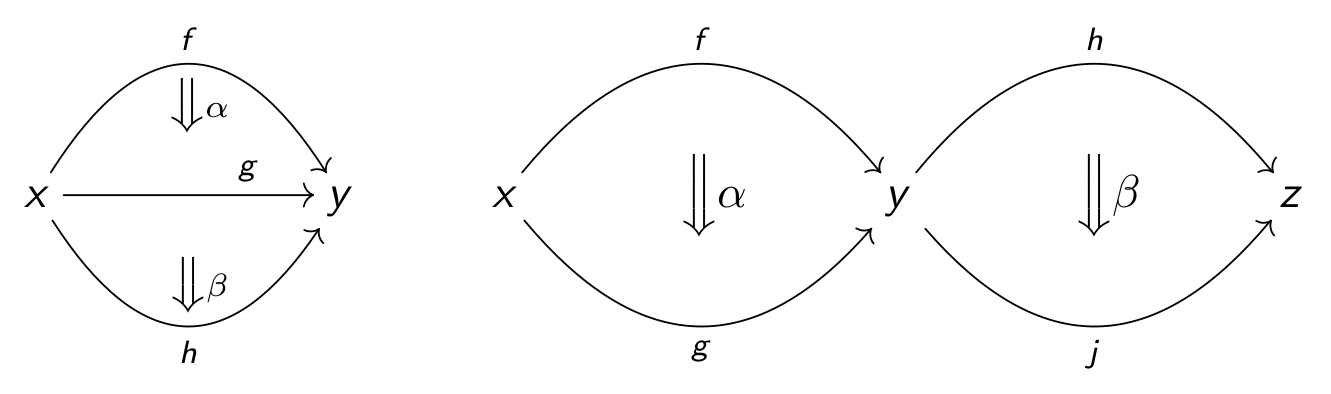
Some basic examples of (strict and weak) 2-categories are:

• The 2-category of categories CAT, i.e. objects are categories, 1-cells are functors and 2-cells are natural transformations.
• The Bimodule 2-category BiMOD i.e. objects are rings \(R,S,T,\dots\), 1-cells are bimodules over two rings \({}_RM_S,{}_RN_S,\dots\) and 2-cells are bimodule homomorphisms. The one-dimensional composition is given by “tensoring over the middle ring” (e.g. \({}_RM_S\otimes_S{}_SN_T\)) and the two-dimensional compositions are standard composition and “tensoring of morphisms”.
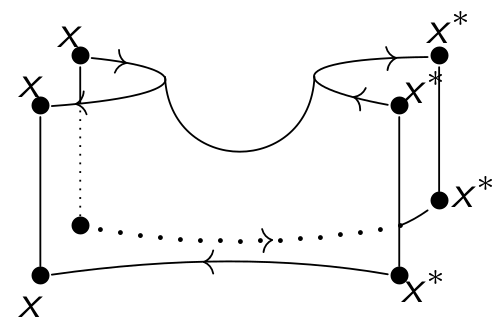
• Two-dimensional cobordism 2-categories, e.g. one can take points as objects, one-dimensional cobordisms as 1-cells and two-dimensional cobordisms as 2-cells.
  

A \((n,r)\)-category is defined in the spirit from above. It consists of possible non-trivial k-cells for \(k\leq n\) and only k-cells for \(k\leq r\) are allowed to be non-invertible. For example a \((1,0)\)-category is a groupoid and, more general, a \((n,0)\)-category is a n-groupoid. Of course, it is possible to consider the limits \(n,r\to\infty\).