Data

• Title: Quivers for \(\mathrm{SL}_{2}\) tilting modules
• Authors: Daniel Tubbenhauer and Paul Wedrich
• Status: Represent. Theory 25 (2021), 440-480. Last update: Mon, 31 May 2021 06:37:56 UTC
• ArXiv link: https://arxiv.org/abs/1907.11560
• ArXiv version = 0.99 published version
• LaTex Beamer presentation: Slides, Slides2, Slides3

Abstract

Using diagrammatic methods, we define a quiver algebra depending on a prime \(\mathsf{p}\) and show that it is the algebra underlying the category of tilting modules for \(\mathrm{SL}_{2}\) in characteristic \(\mathsf{p}\). Along the way, we obtain a presentation for morphisms between \(\mathsf{p}\)-Jones-Wenzl projectors.

A few extra words

Let \(\mathbb{K}\) denote an algebraically closed field and \(\mathbf{Tilt}=\mathbf{Tilt}\big(\mathrm{SL}_{2}(\mathbb{K})\big)\) the additive, \(\mathbb{K}\)-linear category of (left-)tilting modules for the algebraic group \(\mathrm{SL}_{2}=\mathrm{SL}_{2}(\mathbb{K})\). This category can be described as the full subcategory of \(\mathrm{SL}_{2}\)-modules which is monoidally generated by the vector representation \(T(1)\cong\mathbb{K}^{2}\), and which is closed under taking finite direct sums and direct summands.
The purpose of this paper is to give a generators and relations presentation of \(\mathbf{Tilt}\) by identifying it with the category of projective modules for an explicitly described quiver algebra. For \(\mathbb{K}\) of characteristic zero this is trivial as \(\mathbf{Tilt}\) is semisimple, and the indecomposable tilting modules are indeed the simple modules. The quantum analog at a complex root of unity is related to the zigzag algebra with vertex set \(\mathbb{N}\) and a starting condition.
The focus of this paper is on the case of positive characteristic \(\mathsf{p}>0\), for which we represent \(\mathbf{Tilt}\) as a quotient \(Z=Z_{\mathsf{p}}\) of the path algebra of an infinite, fractal-like quiver, a truncation of which is illustrated for \(\mathsf{p}=3\) as

This illustrates the full subquiver containing the first 100 vertices of the quiver underlying \(Z_{3}\).
Note that the algebra \(Z\) contains information about the representation theory of \(\mathrm{SL}_{2}\), as e.g. about the Weyl factors \(\Delta(w_{i}-1)\) in \(T(v-1)\). If the \(\mathsf{p}\)-adic expansion \(v=\sum_{i=0}^{j}a_{i}\mathsf{p}^{i}\) has exactly r+1 non-zero digits, then there are \(2^{r}\) such factors and, correspondingly, r arrows from v-1 to certain \(w_{i}-1 Note further the uniform behavior of \(Z\) with respect to \(\mathsf{p}\). For example

is (a cut-off) of the quivers \(Z_{2}\), \(Z_{5}\) and \(Z_{7}\), which, zooming out such that the precise labels get invisible, look basically the same as the one for \(Z_3\).
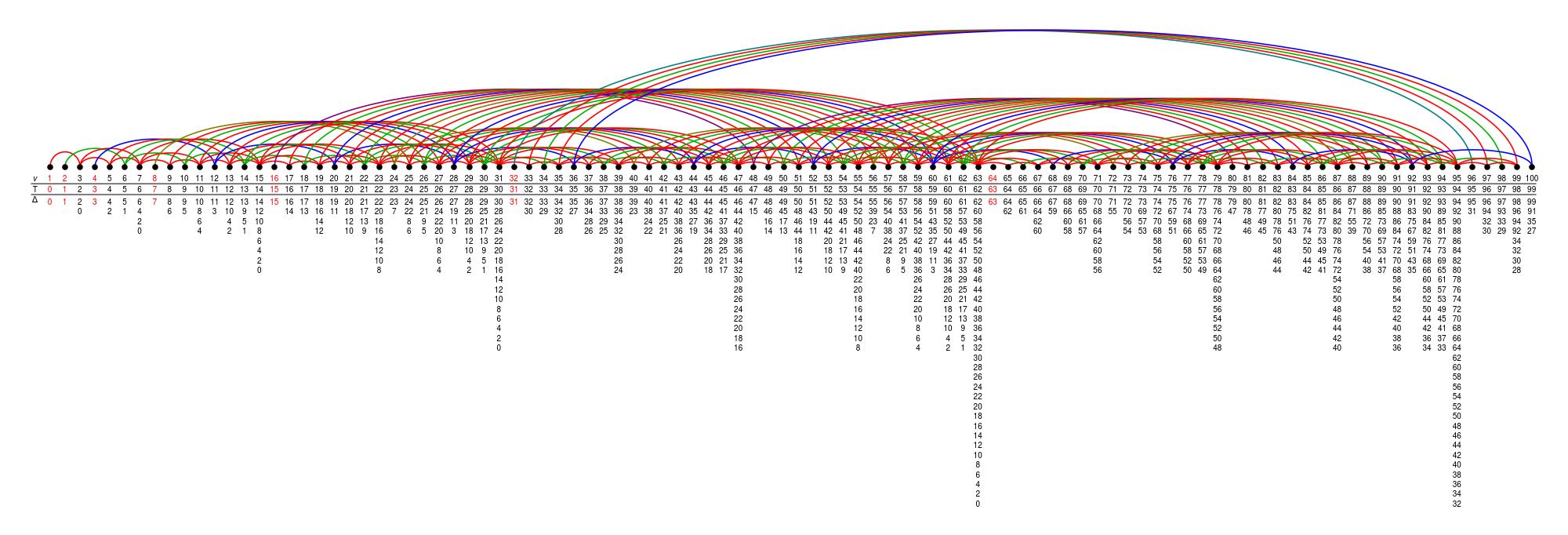
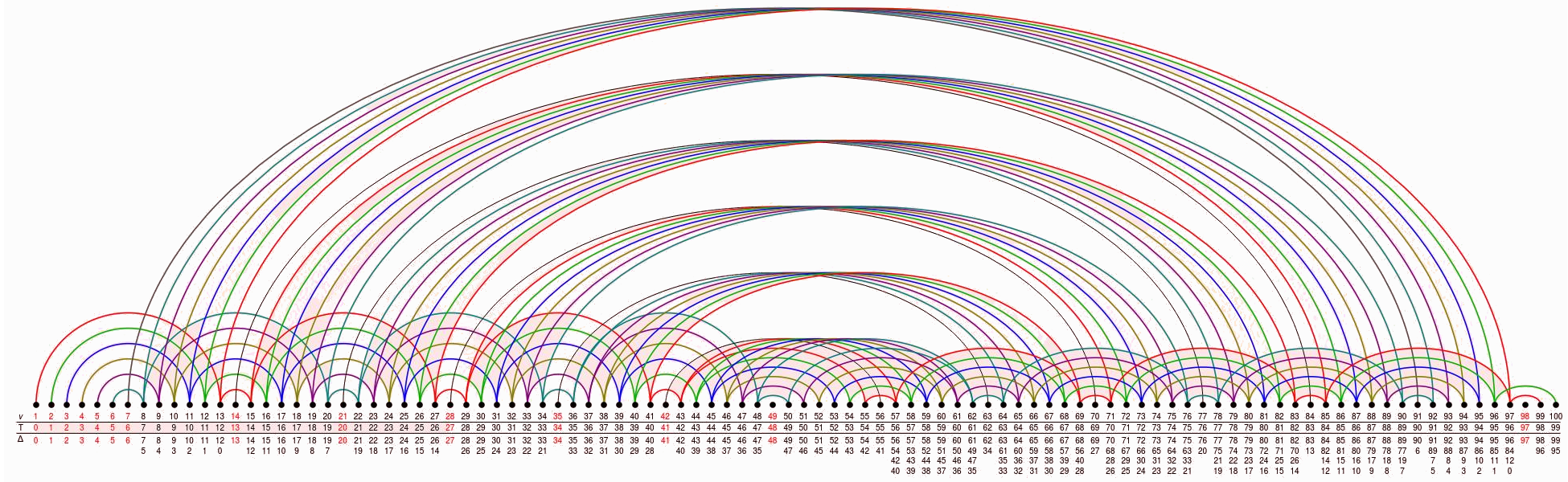
The basis for our work is the classical fact that the Temperley-Lieb algebra controls the finite-dimensional representation theory of \(\mathrm{SL}_{2}\). The second main ingredient is an explicit description of \(\mathsf{p}\)-Jones--Wenzl projectors, which are characteristic \(\mathsf{p}\) analogs of the classical Jones-Wenzl projectors.
The bulk of this paper is devoted to a careful study of morphisms between \(\mathsf{p}\)-Jones--Wenzl projectors over \(\mathbb{F}_{\mathsf{p}}\) and the linear relations between them; a result of which we think as being of independent interest.