Data
- Title: The center of \(\mathrm{SL}_{2}\) tilting modules
- Authors: Daniel Tubbenhauer and Paul Wedrich
- Status: Glasg. Math. J. 64 (2022), no. 1, 165-184. Last update: Mon, 25 Jan 2021 09:24:25 UTC
- ArXiv link: https://arxiv.org/abs/2004.10146
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides, Slides2, Slides3
Abstract
In this note we compute the centers of the categories of tilting modules for \(G=\mathrm{SL}_{2}\) in prime characteristic, of tilting modules for the corresponding quantum group at a complex root of unity, and of projective \(G_{g}T\)-modules when g=1,2.
A few extra words
Let \(\mathbb{K}\) denote an algebraically closed field and \(\mathbf{Tilt}=\mathbf{Tilt}(\mathrm{SL}_{2})\) the additive
\(\mathbb{K}\)-linear category of (left-)tilting modules for the algebraic group \(\mathrm{SL}_{2}\).
In this note we compute the (categorical) center \(\mathbf{Z}(\mathbf{Tilt})\)
of \(\mathbf{Tilt}\), using the explicit description of the
Ringel dual of \(\mathrm{SL}_{2}\).
These Ringel duals are quivers living on certain infinite and fractral graphs, and are basically fractal-zigzag-type algebras on these graphs:
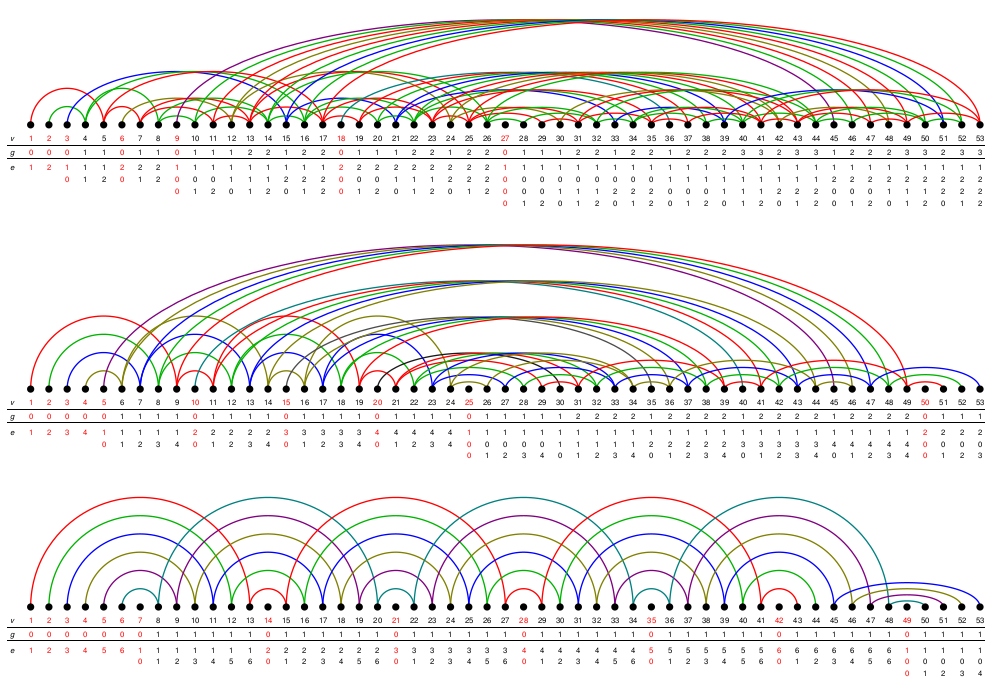
The main theorem then is that we have an (explicit) isomorphism of \(\mathbb{K}\)-algebras between \(\mathbb{K}[X_{v}\mid v\in\mathbb{N}]/\langle X_{v}X_{w}\mid v,w\in\mathbb{N}\rangle\) and \(\mathbf{Z}(\mathbf{Tilt})\).
Finally, we also compute the centers for the category of tilting modules in the quantum group case (which is generation 1) as well as for projective \(G_{g}T\)-modules for g=1,2 (generations 1 and 2), both for \(\mathrm{SL}_{2}\). In these cases the results are similar as for the algebraic group, but much easier and can be thought off as an approximation of order 1 or 2 to the group case.
