Data
- Title: Virtual Khovanov homology using cobordisms
- Author: Daniel Tubbenhauer
- Status: J. Knot Theory Ramifications 23-9 (2014), 91 pages. Last update: Tue, 2 Sep 2014 17:12:36 GMT
- ArXiv link: http://arxiv.org/abs/1111.0609
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1
- Poster: Poster 1 and Poster 2
- Computer talk: MATHEMATICA file and Notebook and Some calculations
Abstract
We give a geometric interpretation of the Khovanov complex for virtual links. Geometric interpretation means that we use a cobordism structure like Bar-Natan, but we allow non orientable cobordisms. Like Bar-Natans geometric complex our construction should work for virtual tangles too. This geometric complex allows, in contrast to the geometric version of Turaev and Turner, a direct extension of the classical Khovanov complex (\(h=t=0\)) and of the variant of Lee (\(h=0,t=1\)). Furthermore we give a classification of all unoriented TQFTs which can be used to define virtual link homologies with this geometric construction.
A few extra words
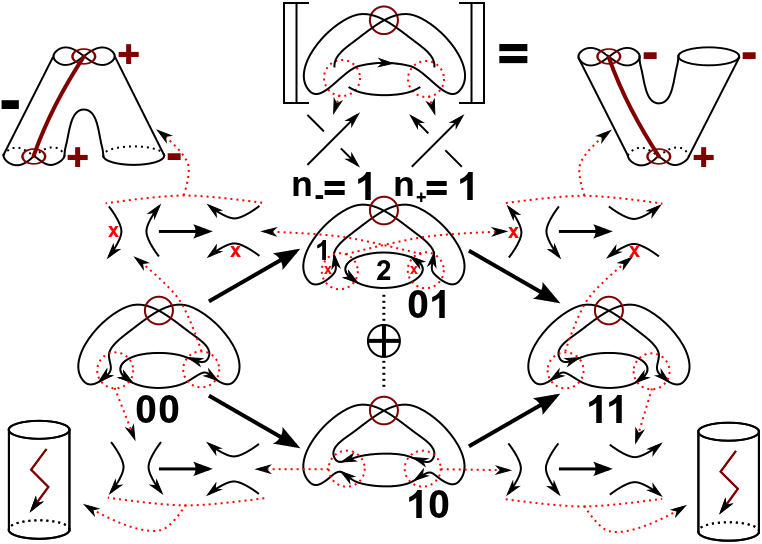
The following picture explains the whole idea. The main ingredient are immersed, possible
non-orientable cobordisms with decorated boundary components, i.e. each boundary of an orientable
gets a decoration from \(\{+,-\}\), and a formal sign, which is either
\(+1\) or \(-1\). All the information
can be read of from local data, i.e. from an a priori chosen orientation of the resolutions and an also
a priori chosen numbering of the circles in the resolutions. Note that different choices lead to the same
complexes modulo chain isomorphisms.
Note that the virtual Khovanov homology is strict stronger then the virtual Jones polynomial, i.e. we show
that there are v-knots with seven crossings with equal v-Jones polynomial, but different v-Khovanov homology.