Data
- Title: Algebraic properties of zigzag algebras
- Authors: Michael Ehrig and Daniel Tubbenhauer
- Status: Comm. Algebra 48 (2020), no.1, 11-36. Last update: Tue, 2 Jul 2019 11:28:16 UTC
- ArXiv link: https://arxiv.org/abs/1807.11173
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1
Abstract
We give necessary and sufficient conditions for zigzag algebras and certain generalizations of them to be (relative) cellular, quasi-hereditary or Koszul.
A few extra words
Let \(\mathrm{Z}_{\rightleftarrows}=\mathrm{Z}_{\rightleftarrows}(\Gamma)\) be the zigzag algebra
associated to a finite, connected, simple graph \(\Gamma\).
The purpose of this
note is to show the following.
Theorem A
\(\mathrm{Z}_{\rightleftarrows}\) is cellular if and only if
\(\Gamma\) is a finite type \(\mathsf{A}\) graph.
\(\mathrm{Z}_{\rightleftarrows}\) is relative cellular if and only if
\(\Gamma\) is a finite or affine type \(\mathsf{A}\) graph.
Further, in all cases where \(\mathrm{Z}_{\rightleftarrows}\) is
(relative) cellular, the path length
endows it with the structure of a graded
(relative) cellular algebra.
Theorem B
\(\mathrm{Z}_{\rightleftarrows}\) is never quasi-hereditary.
Theorem C
\(\mathrm{Z}_{\rightleftarrows}\) is Koszul if and only if \(\Gamma\) is not a
type \(\mathsf{ADE}\) graph.
Moreover, in all cases we construct the corresponding data explicitly.
Let further \(\mathrm{Z}_{\rightleftarrows}^{\mathtt{B}}=\mathrm{Z}_{\rightleftarrows}^{\mathtt{B}}(\Gamma)\) be the
zigzag algebra with a vertex-loop condition (vertex condition for short)
set of vertices \(\mathtt{B}\neq\emptyset\).
Using the same ideas
as for \(\mathrm{Z}_{\rightleftarrows}\) we can also prove:
Theorem A\(\mathtt{B}\)
\(\mathrm{Z}_{\rightleftarrows}^{\mathtt{B}}\) is cellular if and only if
\(\Gamma\) is a finite type \(\mathsf{A}\) graph and the
vertex condition is imposed on one leaf.
\(\mathrm{Z}_{\rightleftarrows}^{\mathtt{B}}\) is relative cellular in exactly the same cases.
Theorem B\(\mathtt{B}\)
\(\mathrm{Z}_{\rightleftarrows}^{\mathtt{B}}\) is quasi-hereditary if and only
if \(\Gamma\) is a finite type \(\mathsf{A}\) graph and the
vertex condition is imposed on one leaf.
Theorem C\(\mathtt{B}\)
\(\mathrm{Z}_{\rightleftarrows}^{\mathtt{B}}\) is always Koszul.
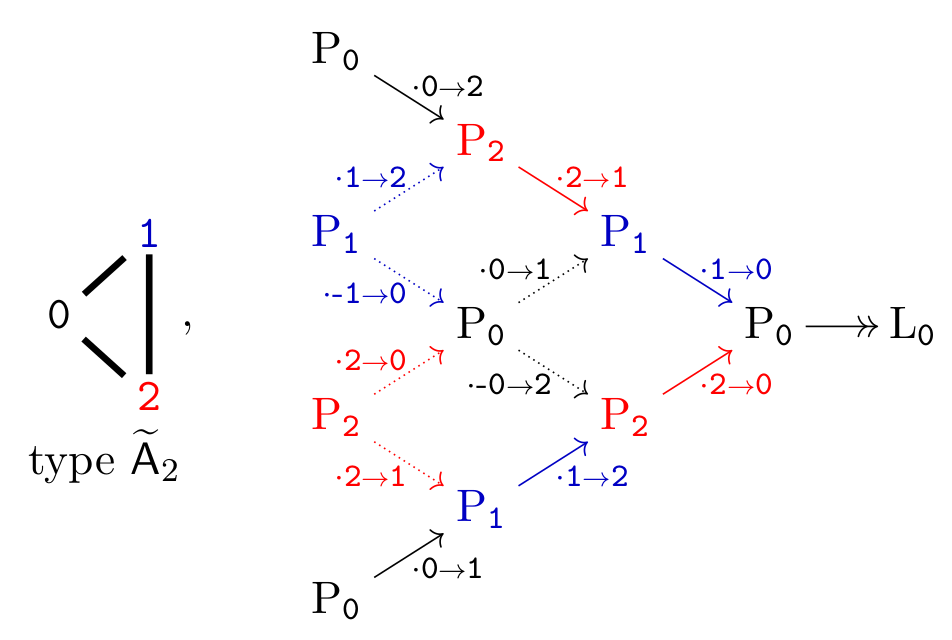
Here is an example of how a linear projective resolution might look like: