Data

• Title: Webs and q-Howe dualities in types \(\mathbf{B}\mathbf{C}\mathbf{D}\)
• Authors: Antonio Sartori and Daniel Tubbenhauer
• Status: Trans. Amer. Math. Soc. 371 (2019), no. 10, 7387-7431. Last update: Tue, 3 Apr 2018 13:17:55 EST
• ArXiv link: https://arxiv.org/abs/1701.02932
• ArXiv version = 0.99 published version
• LaTex Beamer presentation: Slides1, Slides2

Abstract

We define web categories describing intertwiners for the orthogonal and symplectic Lie algebras, and, in the quantized setup, for certain orthogonal and symplectic coideal subalgebras. They generalize the Brauer category, and allow us to prove quantum versions of some classical type \(\mathbf{B}\mathbf{C}\mathbf{D}\) Howe dualities.

A few extra words

Consider the following question: Given some Lie algebra \(\mathfrak{g}\), can one give a generator-relation presentation for the category of its finite-dimensional representations, or for some well-behaved subcategory?
Maybe the best-known instance of this is the case of the monoidal category generated by the vector representation of (quantum) \(\mathfrak{sl}_2\). Its generator-relation presentation is known as the Temperley-Lieb category and goes back to work of Rumer-Teller-Weyl and Temperley-Lieb.
Several generalizations of this were found over the years. The most important one for our paper was seminal work of Cautis-Kamnitzer-Morrison who a generator-relation presentation of the monoidal category generated by (quantum) exterior powers of the vector representation of quantum \(\mathfrak{gl}_n\).
Their crucial observation was that a classical tool from representation and invariant theory, known as skew Howe duality, can be quantized and used as a device to describe intertwiners of quantum \(\mathfrak{gl}_n\). The diagrammatic presentation is provided by so-called (type) \(\mathbf{A}\)-web categories.
The idea which started this paper was to apply Cautis-Kamnitzer-Morrison's approach to types \(\mathbf{B}\mathbf{C}\mathbf{D}\). However, quantization outside of type \(\mathbf{A}\) turns out be be quite delicate. In particular, we cannot use the road map given by Cautis-Kamnitzer-Morrison since quantization of Howe's classical dualities in types \(\mathbf{B}\mathbf{C}\mathbf{D}\) is not a straightforward affair.
To overcome this problem, we consider alternative quantizations in types \(\mathbf{B}\mathbf{C}\mathbf{D}\) provided by so-called coideal subalgebras of quantum \(\mathfrak{gl}_n\). (In short, these have “nicer” quantum factors than the quantum enveloping algebras, but worse “topological behaviour”.)
Our approach then goes as follows: In order to quantize Howe dualities in types \(\mathbf{B}\mathbf{C}\mathbf{D}\), we define extended web categories, which we call cup- and dot-web categories, and prove that they act on the representation categories of the coideal subalgebras. (And they provide diagrammatic descriptions of these categories by playing the roles of “thickened” Brauer categories.) We will then show that these extended web categories can be used to recovering some versions of quantum Howe duality in types \(\mathbf{B}\mathbf{C}\mathbf{D}\).
Note that our approach goes somehow the opposite way with respect to Cautis-Kamnitzer-Morrison's road map: instead of using quantum Howe duality to obtain a web calculus, we use our web categories to prove quantized Howe dualities. We define these cup- and dot-web categories in our paper. All the reader needs to know about them before looking into the paper is summarized in the Figure below.

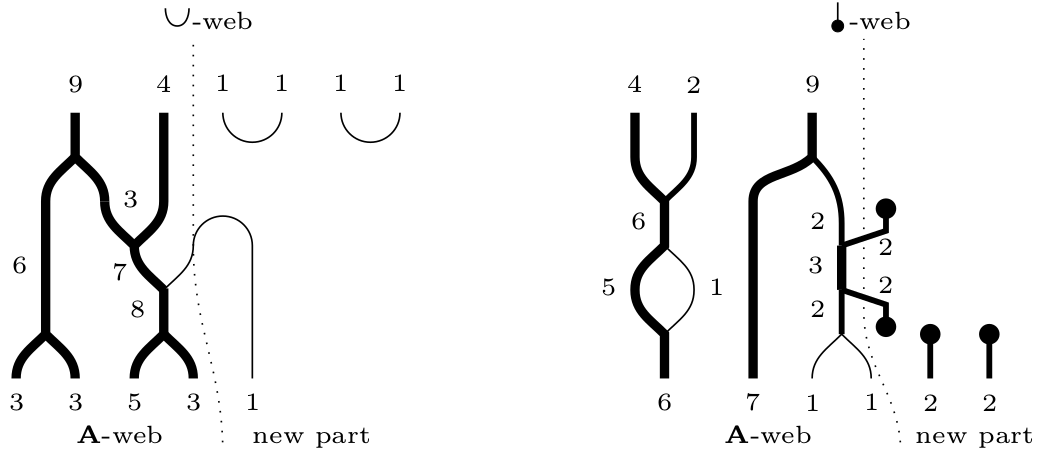
Note that these can be seen as “extended type \(\mathbf{A}\) webs”.