Data
- Title: Annular webs and Levi subalgebras
- Authors: Abel Lacabanne, Daniel Tubbenhauer and Pedro Vaz
- Status: J. Comb. Algebra 7 (2023), no. 3/4, pp. 283-326. Last update: Thu, 9 Nov 2023 08:06:59 UTC
- ArXiv link: https://arxiv.org/abs/2204.00947
- ArXiv version = 0.99 published version
Abstract
For any Levi subalgebra of the form \(\mathfrak{l}=\mathfrak{gl}_{l_{1}}\oplus\dots\oplus \mathfrak{gl}_{l_{d}}\subseteq\mathfrak{gl}_{n}\) we construct a quotient of the category of annular quantum \(\mathfrak{gl}_{n}\) webs that is equivalent to the category of finite dimensional representations of quantum \(\mathfrak{l}\) generated by exterior powers of the vector representation. This can be interpreted as an annular version of skew Howe duality, gives a description of the representation category of \(\mathfrak{l}\) by additive idempotent completion, and a web version of the generalized blob algebra.
A few extra words
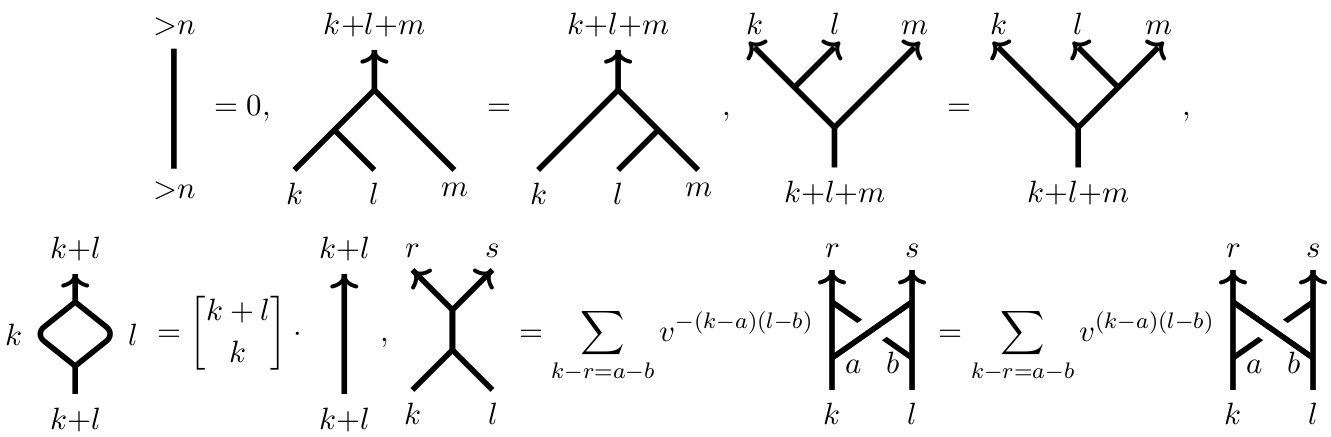
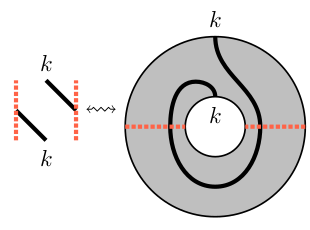
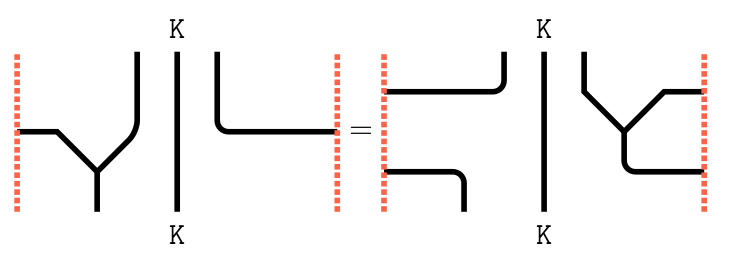
The so-called Schur-Weyl duality has played a key role ever since the early days of representation theory. It relates representations of the symmetric group \(S_m\) and the general linear group \(\mathrm{GL}_{n}=\mathrm{GL}_{n}(\mathbb{C})\), and has been generalized in many ways. The representation used to related these two groups is \((\mathbb{C}^{n})^{\otimes m}\). Let \(\mathrm{L}_=\mathrm{GL}_{l_1}\times\dots \times\mathrm{GL}_{l_d}\subseteq\mathrm{GL}_{n}\), and let us for simplicity stay over \(\mathbb{C}\) for now. Two generalizations of Schur-Weyl duality are of crucial importance for this paper. Firstly, the Schur-Weyl duality of \((\mathbb{Z}/d\mathbb{Z})\wr S_m\) (that is, type \(G(d,1,m)\)) and \(\mathrm{L}\). Here the underlying representation is again \((\mathbb{C}^{n})^{\otimes m}\). Second, skew (type A) Howe duality relating \(\mathrm{GL}_{N}\) and \(\mathrm{GL}_{n}\) via their action on \({\textstyle\bigwedge^{\bullet}}(\mathbb{C}^{N}\otimes\mathbb{C}^{n})\). A diagrammatic interpretation of skew Howe duality is given by (exterior \(\mathrm{GL}_{n}\)) webs. (The same diagrammatics goes under many names, including birdtracks or spiders.) In some sense, in terms of webs, skew Howe duality relating \(\mathrm{GL}_{\bullet}\) and \(\mathrm{GL}_{n}\) takes the form of an equivalence between the category of webs and the category of \(\mathrm{GL}_{n}\)-representations generated by \(\{{\textstyle\bigwedge^{k}}\mathbb{C}^{n}|k\in\{1,\dots,n\}\}\), with the web category being obtained by using all \(\mathrm{GL}_{N}\) for \(N\in\mathbb{N}\). After additive idempotent completion webs even give a diagrammatic interpretation of all finite dimensional \(\mathrm{GL}_{n}\)-representations. In this paper we show that an explicit quotient of the category of annular (exterior \(\mathrm{GL}_{n}\)) webs is equivalent to the category of \(\mathrm{L}\)-representations generated by \(\{{\textstyle\bigwedge^{k}}\mathbb{C}^{n}|k\in\{1,\dots,n\}\}\). As before, additive idempotent completion gives a description of all finite dimensional \(\mathrm{L}\)-representations. This, in some sense, is a form of what could be called annular skew Howe duality (we avoid the notion affine as its meaning is context depending) or skew type \(G(d,1,\bullet)\) Howe duality. The main categories under study is the diagrammatic category of \(\mathrm{GL}_{n}\) webs, with a web being locally of the form