Data
- Title: Diagrammatics for dicyclic groups
- Authors: Peter DeBello and Daniel Tubbenhauer
- Status: preprint. Last update: Mon, 16 Dec 2024 22:11:58 UTC
- ArXiv link: https://arxiv.org/abs/2412.12376
Abstract
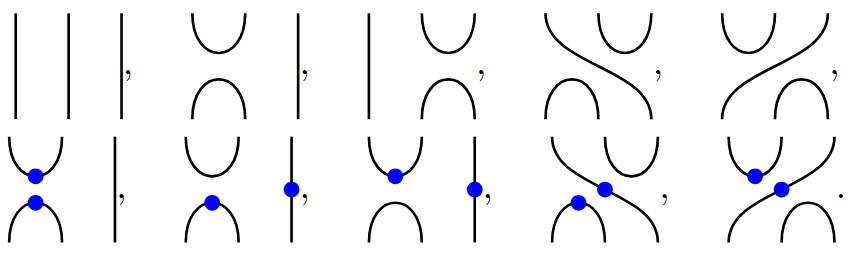
Using that the dicyclic group is the type D subgroup of SU(2), we extend the Temperley–Lieb diagrammatics to give a diagrammatic presentation of the complex representation theory of the dicylic group.
A few extra words
The finite subgroups of SU(2) are given by the ADE classification, and by the McKay correspondence their representation theory differs from SU(2) according to
their affine Dynkin diagrams of ADE type. Since finite groups have finitely many simple representations,
this equivalence no longer holds when one restricts to a finite subgroup of SU(2). A natural question one may ask is therefore: for finite
subgroups of types A, D, or E, how does the Temperley–Lieb category change?
The finite subgroup of SU(2) corresponding to type A is a \(\mathbb{Z}/2\mathbb{Z}\) extension of the cyclic group, so every simple is one dimensional and the description of
the category of its representation is rather trivial. Turning to the next case, in this paper, we answer this question in the case of the type D subgroups
of SU(2), called dicyclic groups, which are \(\mathbb{Z}/2\mathbb{Z}\) extensions of dihedral groups. We examine the case of the infinite dicyclic group, denoted \(\text{Dic}_{\infty}\), as well as the finite dicyclic group of degree n,
denoted \(\text{Dic}_n\). We show that morphisms in the category of representations of the infinite dicyclic group \(\text{Dic}_{\infty}\) are described by a certain type of decorated Temperley–Lieb diagrams.