Data
- Title: Singular TQFTs, foams and type \(\mathrm{D}\) arc algebras
- Authors: Michael Ehrig, Daniel Tubbenhauer and Arik Wilbert
- Status: Doc. Math. 24, 1585-1655 (2019). Last update: Thu, 12 Sep 2019 08:48:07 UTC
- ArXiv link: https://arxiv.org/abs/1611.07444
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1, Slides2
Abstract
We combinatorially describe the 2-category of singular cobordisms, called (rank one) foams, which governs the functorial version of Khovanov homology. As an application we topologically realize the type \(\mathrm{D}\) arc algebra using this singular cobordism construction.
A few extra words
In this paper we study the
web algebra \(\mathfrak{W}\) attached to \(\mathfrak{gl}_2\).
The algebra \(\mathfrak{W}\) naturally appears in the
setup of singular TQFTs in the sense
that its bimodule 2-category
is equivalent to the 2-category
of certain singular surfaces
called foams,
and \(\mathfrak{W}\)
algebraically
controls the functorial version
of Khovanov's link homology.
The 2-category of foams is a sign modified version
of Bar-Natan's original cobordism
(``\(\mathfrak{sl}_2\)-foam'') 2-category
attached to Khovanov's link and tangle invariant.
The signs are crucial for
making Khovanov's link homology functorial, but very delicate
to compute in practice. Our first main result
can be seen as a combinatorial way to compute these signs,
i.e. we define a combinatorial, planar model \(c\mathfrak{W}\) of \(\mathfrak{W}\).
Next, we know that \(\mathfrak{W}\) topologically
controls
the principal block of the parabolic
BGG category \(\mathcal{O}\) of
type \(\mathrm{A}_m\) with parabolic of
type \(\mathrm{A}_{p}\times\mathrm{A}_{q}\) for p+q=m.
This follows since Khovanov's original
arc algebra is a subalgebra of \(\mathfrak{W}\).
There is a type \(\mathrm{D}\) generalization \(\mathfrak{A}\) of Khovanov's
arc algebra, called the type \(\mathrm{D}\) arc algebra.
The algebra \(\mathfrak{A}\)
controls
the principal block of the parabolic BGG
category \(\mathcal{O}\) of
type \(\mathrm{D}_n\) with parabolic of
type \(\mathrm{A}_{n-1}\).
Our second main result is then that, surprisingly, the
type \(\mathrm{D}\) arc algebra is also a subalgebra of \(\mathfrak{W}\).
Thus, the representation theory of
the web algebra
(and hence, the cobordism 2-category of foams)
controls the functoriality of Khovanov homology and
(certain) parabolic category \(\mathcal{O}\) in types \(\mathrm{A}_n\) and \(\mathrm{D}\).
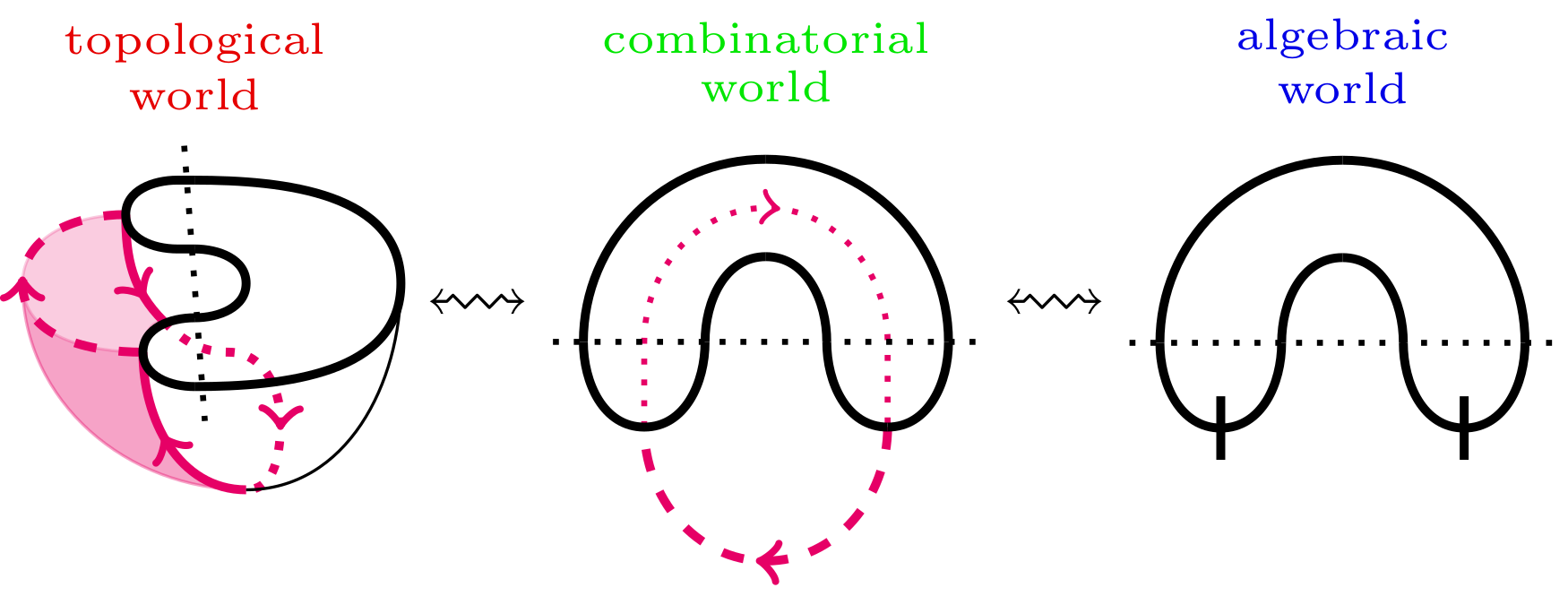
The picture the reader should keep in mind how these
three ``worlds'', represented by elements from
the algebras \(\mathfrak{W}\), \(c\mathfrak{W}\) and \(\mathfrak{A}\)
is: