Research paper

Growth problems in diagram categories

How fast do tensor powers decompose in diagram and interpolation categories? This page is about growth laws behind diagrammatic worlds.

diagram categoriesgrowthtensor powersasymptotics
codearXivlinklink

Data

  • Title: Growth problems in diagram categories
  • Authors: Jonathan Gruber and Daniel Tubbenhauer
  • Status: Bull. Lond. Math. Soc. 57 (2025), no. 11, 3454--3469. Last update: Tue, 29 Jul 2025 06:03:31 UTC
  • Code / errata: Click
  • arXiv: http://arxiv.org/abs/2503.00685
  • More details: Clickclick

Abstract

In the semisimple case, we derive (asymptotic) formulas for the growth rate of the number of summands in tensor powers of the generating object in diagram/interpolation categories.

What is the point?

In many diagram categories one can multiply an object with itself again and again. The question is not only what appears, but how quickly the number of pieces grows. This paper turns that counting problem into a systematic comparison of exponential and superexponential behavior.

Objects:
take tensor powers of one generator.
Counting:
track indecomposable summands.
Asymptotics:
separate tame growth from wild growth.

More details

We begin with the following table, the meaning of which we will explain shortly:

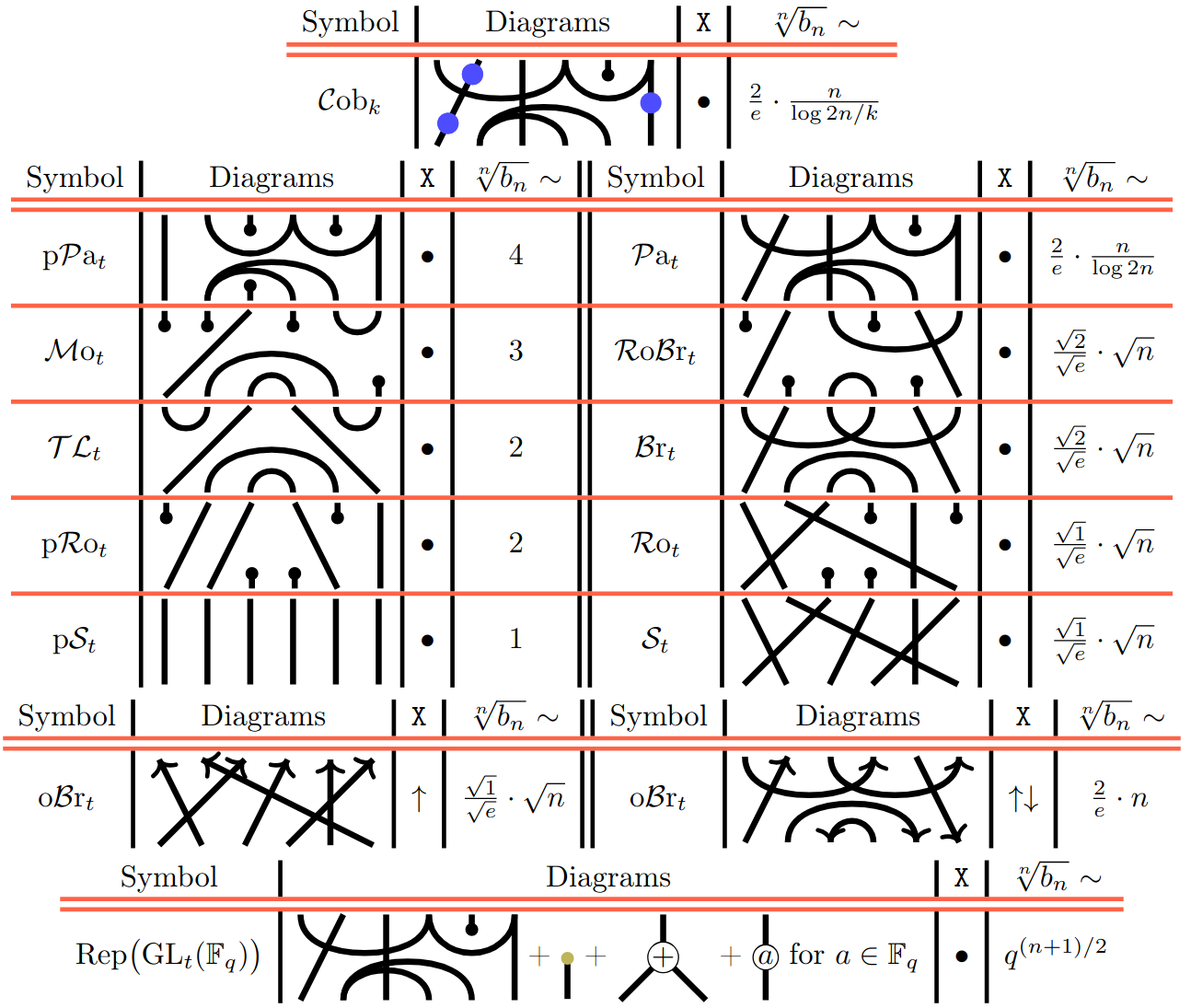
Let \(C\) be an additive Krull–Schmidt monoidal category. Let \(X\in C\) be an object of \(C\). We define \[ b_{n}=b_{n}^{C,X}:=\#\text{indecomposable summands in \(X^{\otimes n}\) counted with multiplicities}. \] We identify the sequence \(b_{n}\) with its function \(n\mapsto b_{n}\).
The function \(b_{n}\) has been the subject of extensive study. In particular, in well-behaved categories, such as finite-dimensional representations of a group one has \[ \lim_{n\to\infty}\sqrt[n]{b_{n}}\in\mathbb{R}_{\geq 1}, \quad\text{exponential growth} \] which shows that \(b_{n}\) grows exponentially. In contrast, some still well-structured categories exhibit superexponential growth, meaning that \[ \sqrt[n]{b_{n}}\text{ is unbounded,} \quad\text{superexponential growth}. \] We study the asymptotic behavior of \(\sqrt[n]{b_{n}}\) in the above diagram categories, all in the semisimple situation (all parameters are generic) and over the complex numbers.