Data
- Title: Asymptotics in infinite monoidal categories
- Authors: Abel Lacabanne, Daniel Tubbenhauer and Pedro Vaz
- Status: preprint. Last update: Mon, 15 Apr 2024 07:16:52 UTC
- Code and (possibly empty) Erratum: Click
- ArXiv link: https://arxiv.org/abs/2404.09513
Abstract
We discuss formulas for the asymptotic growth rate of the number of summands in tensor powers in certain (finite or infinite) monoidal categories. Our focus is on monoidal categories with infinitely many indecomposable objects, with our main tools being generalized Perron–Frobenius theory alongside techniques from random walks.
A few extra words
This paper is a generalization of this paper
and essentially everything we do in that paper works in the setting of infinite categories as well, with one key catch:
the categories need to satisfy additional conditions.
An example of such a condition is that the simple random walk on the fusion graph associated to the problem in question is positively recurrent.
This, roughly speaking, means that random walks return to the starting point with probability \(1\).
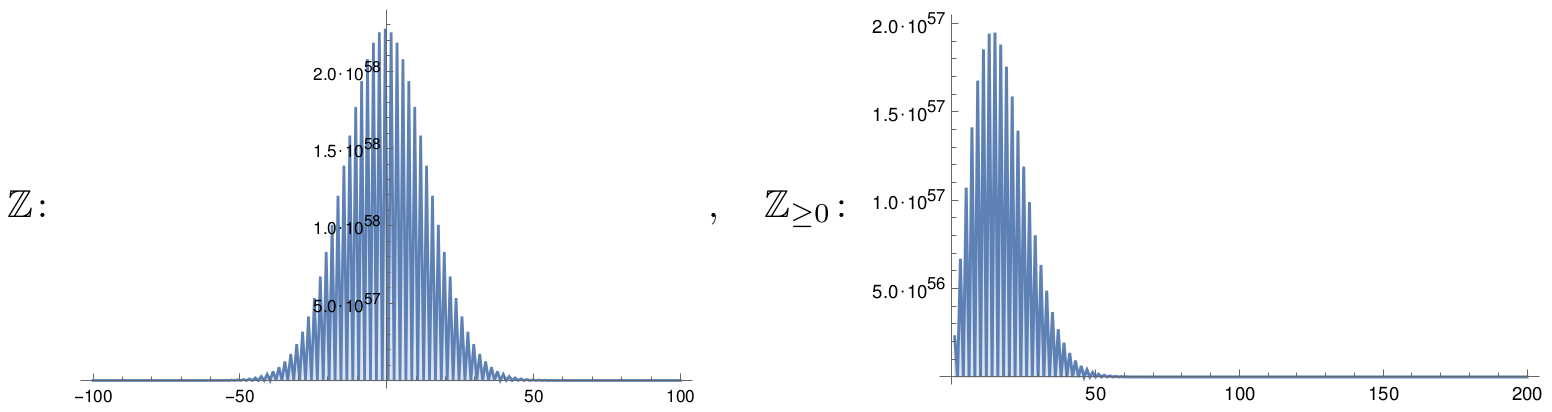
Let us illustrates this in two example: the random walk on \(\mathbb{Z}\), which is positively recurrent, and the random walk on \(\mathbb{N}=\mathbb{Z}_{\geq 0}\), which is not positively recurrent.
The difference becomes evident when one looks at the number of path of length \(n\) starting at the origin, and ending at vertex
\(v\). For \(n=200\), plotting this in \(x,y\)-coordinates \((\text{end vertex},\text{number of paths})\) gives:
