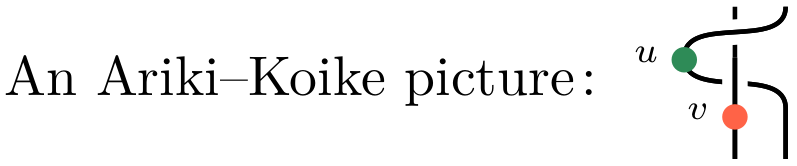Handlebody diagram algebras
In this paper we study handlebody versions of some classical diagram algebras, most prominently, handlebody versions of Temperley-Lieb, blob, Brauer, BMW, Hecke and Ariki-Koike algebras.
Data
- Title: Handlebody diagram algebras
- Authors: Daniel Tubbenhauer and Pedro Vaz
- Status: Rev. Mat. Iberoam. 39 (2023), no. 3, pp. 845-896.
- arXiv link: https://arxiv.org/abs/2105.07049
- arXiv version = 0.99 published version
- LaTeX Beamer presentation: Slides
Abstract
In this paper we study handlebody versions of some classical diagram algebras, most prominently, handlebody versions of Temperley-Lieb, blob, Brauer, BMW, Hecke and Ariki-Koike algebras. Moreover, motivated by Green-Kazhdan-Lusztig's theory of cells, we reformulate the notion of (sandwich, inflated or affine) cellular algebras. We explain this reformulation and how all of the above algebras are part of this theory.
What is the point?
In this paper we study handlebody versions of some classical diagram algebras, most prominently, handlebody versions of Temperley-Lieb, blob, Brauer, BMW, Hecke and Ariki-Koike algebras.
A picture
A few extra words
Our starting point is a diagrammatic description of handlebody braid groups of genus g, i.e. a diagrammatic description of the configuration space of a disk with g punctures. The picture above shows an example. It illustrates a handlebody braid of genus 4: The three strands on the right are usual strands. The four thick and blue/grayish strands on the left are core strands and they correspond to the punctures of the disk or the cores of the handlebody. A handlebody link is obtained by an appropriate closure, merging the core strands at infinity, as illustrated in the picture above. The core strands correspond to cores of a handlebody, hence the name. There are certain handlebody algebras that we study in this paper, based on the above diagrammatic description:
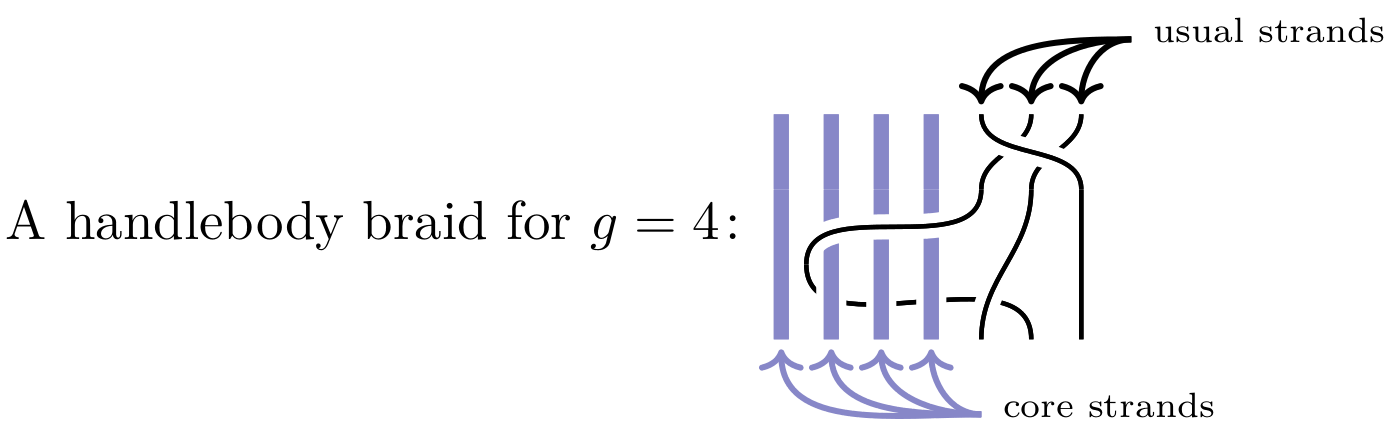
- Handlebody Temperley-Lieb and blob algebras. The pictures to keep in mind are crossingless matchings and core strands (left, Temperley-Lieb) respectively crossingless matchings decorated with colored blobs (right, blob) as shown in the picture above.
- Handlebody Brauer and BMW algebras. These are tangle algebras with core strands The picture above shows an example.
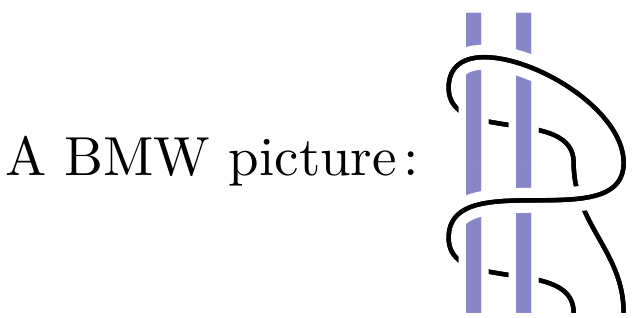
- Handlebody Hecke and Ariki-Koike algebras, illustrated in the picture above.