Data
- Title: HOMFLYPT homology for links in handlebodies via type \(\mathsf{A}\) Soergel bimodules
- Authors: David E.V. Rose and Daniel Tubbenhauer
- Status: Quantum Topol. 12 (2021), no. 2, 373-410. Last update: Mon, 19 Aug 2019 15:31:29 UTC
- ArXiv link: https://arxiv.org/abs/1908.06878
- LaTex Beamer presentation: Slides1, Slides2, Slides3, Slides4, Slides5, Slides6
Abstract
We define a triply-graded invariant of links in a genus g handlebody, generalizing the colored HOMFLYPT (co)homology of links in the 3-sphere. Our main tools are the description of these links in terms of a subgroup of the classical braid group, and a family of categorical actions built from complexes of (singular) Soergel bimodules.
A few extra words
The HOMFLYPT polynomial is a classical invariant of links in the 3-sphere
with interesting and deep connections to representation theory.
The HOMFLYPT polynomial may be defined by using representations of the
classical n strand braid group \(\mathrm{Br}(n)\) on the type A Hecke algebra.
Indeed, we may use Alexander's theorem to present a link as a braid closure,
and the HOMFLYPT polynomial then results by mapping the braid to
the Hecke algebra and
applying the so-called Jones-Ocneanu trace.
Khovanov's categorification of this approach replaces the Hecke algebra by the
corresponding Hecke category, i.e. the category of type A Soergel bimodules.
The latter admits a categorical action of \(\mathrm{Br}(n)\) via so-called Rouquier complexes,
and the link homology results by taking Hochschild (co)homology,
which provides a categorical analog
of the Jones-Ocneanu trace.
In this paper, we remedy this by constructing generalizations of the triply-graded homology for links
in 3-manifolds distinct from the 3-sphere, namely in genus g handlebodies.
(For g=1, this is the case of links in the thickened annulus.)
Our key insights are: (1) to consider various generalizations of the classical braid group that
are related to links in handlebodies,
and (2) that certain structures in categorical representation theory model the topology of the handlebody.
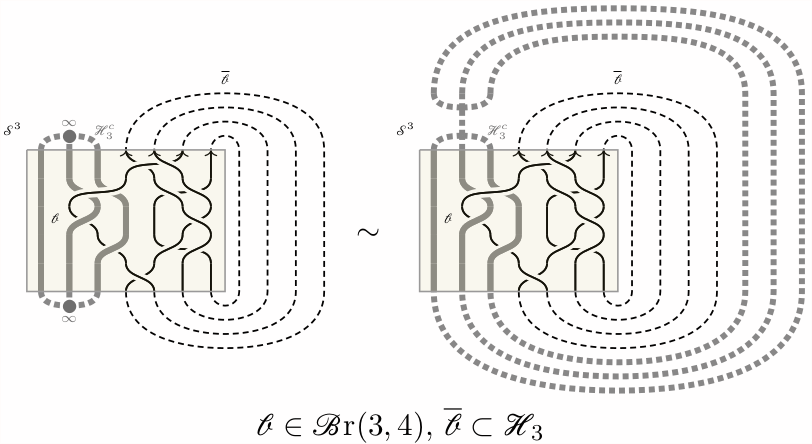
Regarding (1), we consider the genus g handlebody braid \(\mathrm{Br}(g,n)\)
(the classical story here is the g=0 case, where \(\mathrm{Br}(n)=\mathrm{Br}(0,n)\))
for which analogs
of Alexander's and Markov's theorem hold. analogues of Alexander's
and Markov's Theorems hold for links in the genus g handlebody.
Braids in \(\mathrm{Br}(g,n)\) can be pictured as classical braids in the presence of
non-intersecting ``core strands''.
We then obtain a link in a handlebody by allowing the tops and bottoms of the core strands to
meet at \(\infty\), and by taking a closure of the ``usual strands''.
The latter then form a link in the complement of the (glued) core strands,
which is a handlebody.
Regarding (2), it turns out that a slightly adjusted
presentation is more suitable: We expand the point at infinity to a small segment,
which we move close to the top of the core strands.
As a result, we can view the closure of the ``usual strands''
as a link in the handlebody given by the complement
of the graph determined by the core strands and the segment at infinity, e.g.:
Last, but not least, let us mention the relation from \(\mathrm{Br}(g,n)\) to classical Artin-Tits braid groups, which is summarized by

