Data
- Title: Cellularity of KLR and weighted KLRW algebras via crystals
- Authors: Andrew Mathas and Daniel Tubbenhauer
- Status: To appear in Commun. Am. Math. Soc. Last update: Sun, 2 Nov 2025 11:57:39 UTC
- ArXiv link: https://arxiv.org/abs/2309.13867
- Code: Click, Click
Abstract
We prove that the weighted KLRW algebras of finite type, and their cyclotomic quotients, are sandwich cellular algebras. The sandwich cellular bases are explicitly described using crystal graphs. As a special case, this proves that the KLR algebras of finite type are sandwich cellular. As one application, we give explicit formulas for the graded decomposition numbers of the cyclotomic algebras in level one.
A few extra words
In groundbreaking papers, Khovanov–Lauda and Rouquier introduced a family
of algebras attached, now called the KLR or quiver Hecke algebras, to a quiver . Even though there
is large literature on these algebras there is still surprisingly little structural information known about
these algebras. For example, these algebras have certain finite dimensional quotients and bases for these algebras are known only in special cases.
In 2012, Kleshchev, Loubert and Miemietz conjectured that the KLR algebras are graded (affine)
cellular algebras. Some progress was made towards this conjecture for the infinite dimensional KLR
algebras, but the conjecture for the cyclotomic quotients proved
to be much harder, except in affine type A.
In order to understand categorifications of tensor products, Webster introduced the weighted KLRW algebras, which include the KLR algebras as a special case.
Using these algebras, Mathas proved that the weighted KLRW algebras and their cyclotomic quotients are graded (affine) sandwich cellular algebras in
some affine types, extending ideas from Bowman for affine type A.
This paper extends the machinery developed by Mathas to study weighted KLRW algebras, and KLR algebras, of finite type.
By the work of Lauda–Vazirani and Varagnolo–Vasserot, it is known that the cyclotomic KLR algebras of finite type
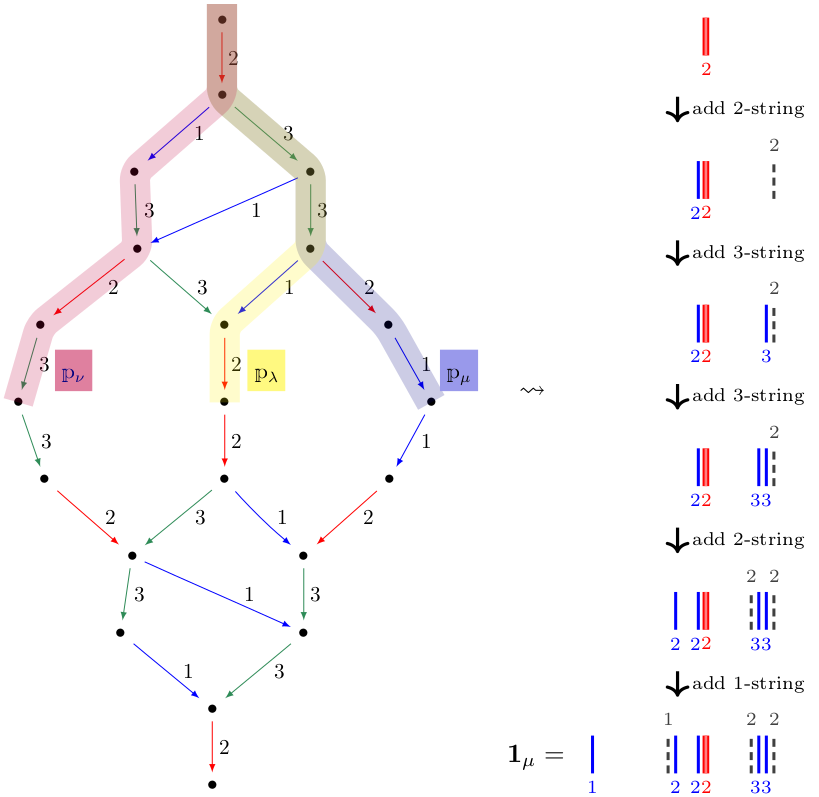
categorify the highest weight modules and their crystal graphs. We use the combinatorics of the crystal graphs to
explicitly describe sandwich cellular bases of the weighted KLRW algebras. In this way we are able to directly link the crystal theory and the KLRW algebras.
Here is an example of how this works: