Data

• Title: Cellularity for weighted KLRW algebras of types \(B\), \(A^{(2)}\), \(D^{(2)}\)
• Authors: Andrew Mathas and Daniel Tubbenhauer
• Status: J. Lond. Math. Soc. (2) 107 (2023), no. 3, 1002-1044. Last update: Sat, 31 Dec 2022 17:26:25 EST
• ArXiv link: https://arxiv.org/abs/2111.12949
• ArXiv version = 0.99 published version
• Some idempotents plus code: A2 as pdf, A2 as tex, D2 as pdf, D2 as tex
• LaTex Beamer presentation: Slides1, Slides2, Slides3, Slides4, Slides5

Abstract

This paper constructs homogeneous affine sandwich cellular bases of weighted KLRW algebras in types \(B_{\mathbb{Z}_{\geq 0}}\), \(A^{(2)}_{2e}\), \(D^{(2)}_{e+1}\). Our construction immediately gives homogeneous sandwich cellular bases for the finite dimensional quotients of these algebras. Since weighted KLRW algebras generalize KLR algebras, we also obtain bases and cellularity results for the (infinite and finite dimensional) KLR algebras.

A few extra words

KLR algebras, or quiver Hecke algebras, are certain graded infinite dimensional algebras attached to a quiver. These algebras arose in categorification and categorical representation theory. They admit finite dimensional quotients, called cyclotomic KLR algebras. Both, KLR algebras and their cyclotomic quotients, play crucial roles in modern representation theory and have attracted a lot of attention since their introduction.
A crucial problem is to determine whether these algebras are (graded) cellular or some variation of cellularity such as affine cellular. It turns out that they tend to be graded affine cellular in the infinite dimensional case and graded cellular in the finite dimensional case. However, to the best of our knowledge and modulo weighted KLRW algebras, there is no clear relationship between the bases for the infinite dimensional algebras and the bases for their finite dimensional quotients. Even better, all of these bases work over any commutative integral domain \(R\) (for example \(R=\mathbb{Z}\)).
Weighted KLRW algebras are generalizations of KLR algebras that were introduced by Webster. Similar to KLR algebras, these algebra also admit finite dimensional quotients. The KLR algebras are subalgebras of the weighted KLRW algebras. One of the key properties of these weighted KLRW algebras is that in the they have homogeneous affine cellular bases constructed in the style of low dimensional topology, and these bases automatically descend to the finite dimensional quotients. As a result, we obtained homogeneous (affine) cellular bases for the corresponding KLR algebras and their finite dimensional quotients.
All of these algebras depend on a quiver. The case of AC types was considered in our previous paper, this paper is concerned about the BAD types. The mentioned types are the following:

Most of the constructions in BAD types are the same as in our previous paper, but there is one crucial difference. The weighted KLRW algebras are not cellular in a natural way, but what we call sandwich cellular. The sandwich part of our bases corresponding to the finite dimensional quotients is given by copies of the dual numbers \(R[X]/(X^{2})\), which explains the powers of 2 appearing in the dimension formulas of the finite dimensional KLR algebras.
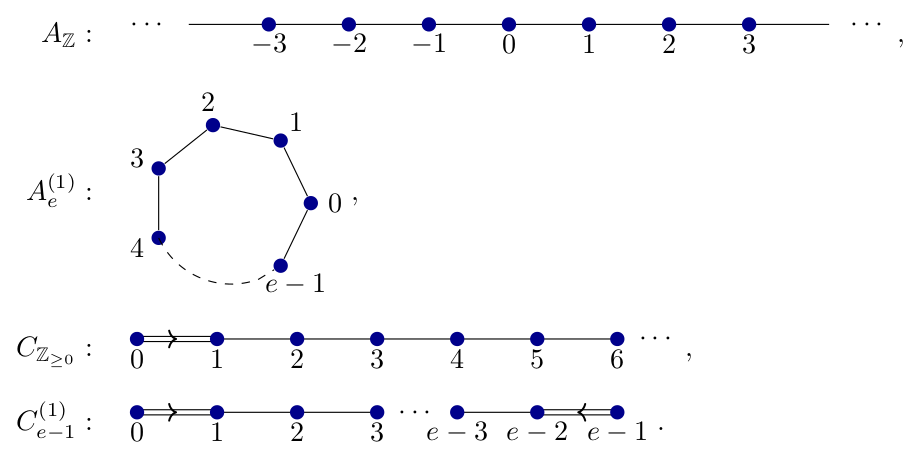
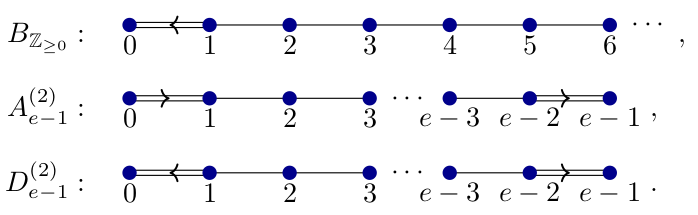
The basis elements are constructed using a certain (dotted idempotent diagram), that is flanked by crossings. This is the typical construction of cellular bases for KLR-type algebras. What is new is that one sandwiches the dual numbers (the finite part) and a polynomial ring (the affine part) in between. The picture to keep in mind how these sandwich cellular bases are constructed is: When going to the finite dimensional quotients only the finite part remains, so we get the aforementioned powers of 2 in the dimension formula.