“Lecture Algebraic topology”

Algebraic topology is a twentieth century field of mathematics that is pervasive across mathematics and the sciences. It is unreasonably successful, being one of the newest fields of mathematics.
One of the most important aims of algebraic topology is to distinguish or classify topological spaces and maps between them up to homeomorphism.
Invariants (data that stays the same under operations on spaces) and obstructions are key to achieve this aim, meaning that \[ \text{invariants different}\Rightarrow\text{spaces different}. \] The converse is however often false, and invariants are stronger the more often the converse holds. However, strong invariants might but hard or impossible to compute, and a good invariant is an invariant which balances between being strong and computable. The main aim of algebraic topology is to associate algebraic data to topological spaces.
Here is an example. The sphere and the torus illustrated below are certainly not the same. But how can we be sure? The algebraic topology approach is to associate to them, say, numbers \(\chi\)
so we conclude that the sphere (left, a balloon) is not the torus (right, an empty donut) by simply observing that \(2\neq 0\). However, the invariant \(\chi\) is not complete in the sense that
but the two topological spaces, the disc and the real projective plane (right, immersed in \(\mathbb{R}^3\)), are not the same. A crucial aim of algebraic topology is thus to have a big enough backpack of invariants to tackle problems in the wild.
A classical and familiar invariant is the Euler characteristic of a topological space (used in the above examples), which was initially discovered via combinatorial methods and has been rediscovered in many different guises. This invariant associates numbers to topological spaces, and is without doubt a good invariant.
Modern algebraic topology goes one step further, and associates more sophisticated invariants to topological spaces. Algebraic topology allows the solution of complicated geometric problems with algebraic methods.
In a nutshell, imagine a closed loop of string that looks knotted in space. How would you tell if you can wiggle it about to form an unknotted loop without cutting the string? The space of all deformations of the loop is an intractable set. The key idea is to associate algebraic structures, such as groups or vector spaces, with topological objects such as knots, in such a way that complicated topological questions can be phrased as simpler questions about the algebraic structures. In particular, this turns questions about an intractable set into a conceptual or finite, computational framework that allows us to answer these questions with certainty.
In this unit you will learn about fundamental group and covering spaces, homology and cohomology theory. These form the basis for applications in other domains within mathematics and other disciplines, such as physics or biology. In fact, one of the strengths of algebraic topology has always been its wide degree of applicability to other fields.
At the end we will have developed skills to determine whether seemingly intractable problems can be solved with topological methods.
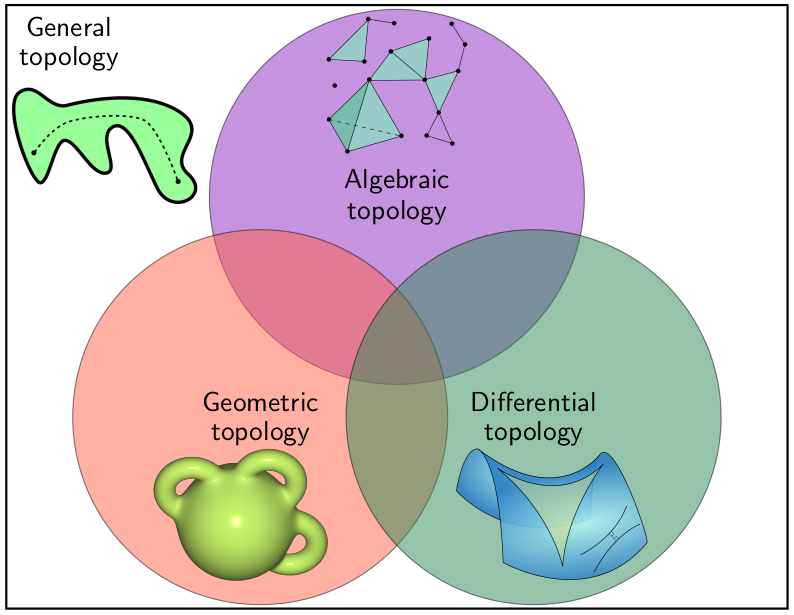
As a final note, there are three main fields of modern topology, with a huge overlap, of course. These fields are algebraic, geometric and differential topology:
All of these are similar in flavor and have the same aims, but use different methods. All of this is embedded into general topology, which provides the underlying language.

Contact

Daniel Tubbenhauer email

Please put [Lecture Algebraic Topology] as the subject.

Who?

Where and when?

Schedule

  1. 09.Aug.2021, Speaker: Daniel Tubbenhauer, Topic: The beginnings - What is...algebraic topology?, Notes: Click, Video: Click
  2. 16.Aug.2021, Speaker: Daniel Tubbenhauer, Topic: Some definitions in topology - Cell complexes and alike, Notes: Click, Video: Click
  3. 23.Aug.2021, Speaker: Daniel Tubbenhauer, Topic: The fundamental group I - The first steps, Notes: Click, Video: Click
  4. 30.Aug.2021, Speaker: Daniel Tubbenhauer, Topic: The fundamental group II - The Seifert-van Kampen theorem, Notes: Click, Video: Click
  5. 06.Sep.2021, Speaker: Daniel Tubbenhauer, Topic: The fundamental group III - Covering spaces, Notes: Click, Video: Click
  6. 13.Sep.2021, Speaker: Daniel Tubbenhauer, Topic: The fundamental group IV - Groups, graphs and \(K(G,1)\) spaces, Notes: Click, Video: Click
  7. 20.Sep.2021, Speaker: Daniel Tubbenhauer, Topic: Homology and cohomology I - Simplicial, singular and cellular homology, Notes: Click, Video: Click
  8. 04.Oct.2021, Speaker: Daniel Tubbenhauer, Topic: Homology and cohomology II - The axiomatic approach, Notes: Click, Video: Click
  9. 11.Oct.2021, Speaker: Daniel Tubbenhauer, Topic: Homology and cohomology III - Cohomology groups, Notes: Click, Video: Click
  10. 18.Oct.2021, Speaker: Daniel Tubbenhauer, Topic: Homology and cohomology IV - The cohomology ring, Notes: Click, Video: Click
  11. 25.Oct.2021, Speaker: Daniel Tubbenhauer, Topic: Homology and cohomology V - Poincaré duality, Notes: Click, Video: Click
  12. 01.Nov.2021, Speaker: Daniel Tubbenhauer, Topic: Whats next? - Some outlook including homotopy, Notes: Click, Video: Click

Exercises

The exercises correspond 1:1 to the talks in the list above.
  1. 09.Aug.2021, Exercise 1, Click
  2. 16.Aug.2021, Exercise 2, Click
  3. 23.Aug.2021, Exercise 3, Click
  4. 30.Aug.2021, Exercise 4, Click
  5. 06.Sep.2021, Exercise 5, Click
  6. 13.Sep.2021, Exercise 6, Click
  7. 20.Sep.2021, Exercise 7, Click
  8. 04.Oct.2021, Exercise 8, Click
  9. 11.Oct.2021, Exercise 9, Click
  10. 18.Oct.2021, Exercise 10, Click
  11. 25.Oct.2021, Exercise 11, Click
  12. 01.Nov.2021, Exercise 12, Click

Exam

If you are on Canvas, you should have seen the following notification (see also Click):
Here is the decryption:
  1. The above is an old photo I took, where the day of the exam is still disclosed. The day is 24.Nov.2021.
  2. Allocated 30 minutes per person, see 1 above. This means 20 minutes of questions, and the remaining 10 minutes are meant as a buffer between the various exams.
  3. In 2 above it is stressed that the time you see on your personal notification is when the exam session starts on that day, not when your exam is. You will receive a personal invitation email/notification in Canvas with your time and a zoom link due in time (roughly a week before the exam). Please log into zoom 5 minutes before it is your term - you will be put in a waiting room.
  4. In 3, ignore the time, see the previous bullet point.
  5. Unfortunately, there was no option to alter the field names Writing Time and Reading Time, see 1 and below. The names should be ignored. The 30 minutes are what is explained in the first point.
  6. The questions will span the three main topics of the lectures: the general setup, the fundamental group and homology.
  7. You will get the results and feedback via Canvas, hopefully on the day of the exam. (I will wait until everyone is done before I decide on a grade.) After the exam there is only a short buffer, so please log out right after the exam.
  8. I will make a recording of the exam, which is not going to get public. (This is to ensure that everything is legit, which is in your favor.)