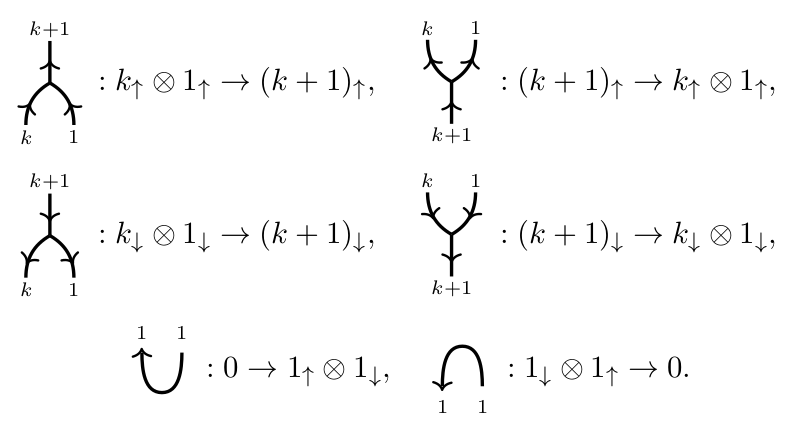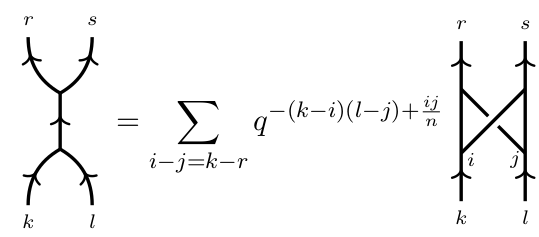Data
- Title: Minimal presentations of \(\mathfrak{gl}_n\)-web categories
- Authors: Genta Latifi and Daniel Tubbenhauer
- Status: preprint. Last update: Thu, 23 Dec 2021 16:32:53 UTC
- ArXiv link: https://arxiv.org/abs/2112.12688
- Note: This is part of the my student Genta's Ph.D. thesis and I do not deserve to be part of the paper - Genta has done all the work! However, Genta insisted that I am, so here we are. I could use the opportunity to blame all mistakes in this paper on Genta. But honestly, any mistake in a Ph.D. thesis is the advisors fault - so I take the blame!
Abstract
In this paper we study categories of \(\mathfrak{gl}_n\)-webs which describe associated representation categories of the quantum group \(\text{U}_{q}(\mathfrak{gl}_n)\). We give a minimal presentation of the category of \(\mathfrak{gl}_n\)-webs over a field with generic quantum parameters. We additionally describe an integral presentation which differs from others in the literature because it is “as coefficient-free as possible”.
A few extra words
Web categories, in various incarnations, are around for donkey's years. They arose in representation theory
in the 1930s (Rumer-Teller-Weyl and Brauer are the big names), but they were popularized
during the rise of quantum topology in the 1980s and 1990s since they give diagrammatic
presentations of representation categories that are at the heart of the Witten-Reshetikhin-Turaev invariants.
This paper studies symmetric and exterior categories of \(\mathfrak{gl}_n\)-webs (strictly speaking
only symmetric one, but the arguments work mutatis mutandis in the exterior case as well), and we discuss minimal
and integral presentations of these categories.
Here is the minimal list of relations: