Growth problems for representations of finite monoids
Growth laws for tensor powers of finite-monoid representations, guided by the group of units and Brauer characters.
Data
- Title: Growth problems for representations of finite monoids
- Authors: David He and Daniel Tubbenhauer
- Status: North-West. Eur. J. Math. 11 (2025), 103–117, i. Last update: Sat, 8 Nov 2025 13:42:37 UTC
- Code / errata: Click
- arXiv: https://arxiv.org/abs/2502.02849
Abstract
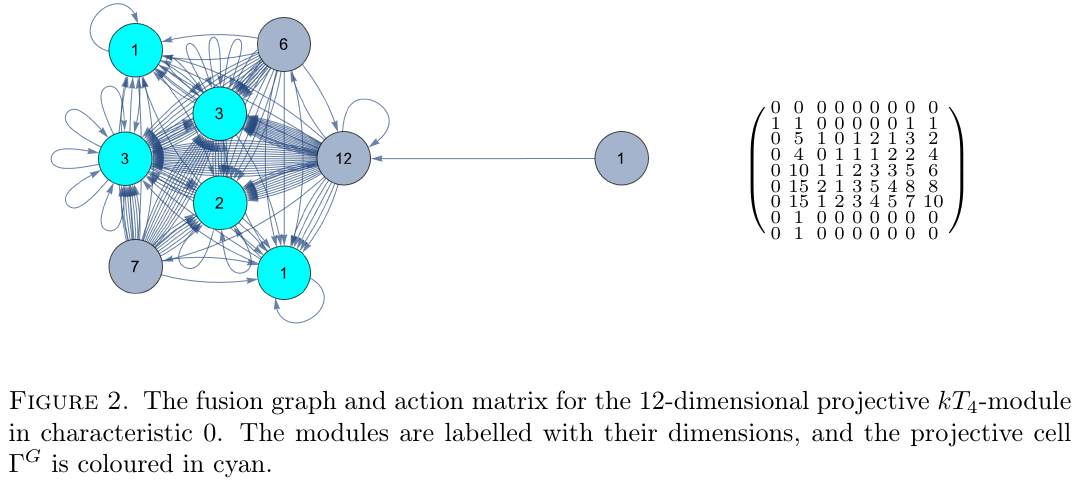
We give a conjecture for the asymptotic growth rate of the number of indecomposable summands in the tensor powers of representations of finite monoids, that it can be obtained from the (Brauer) character table of the monoid's group of units. We prove it under an additional hypothesis. We also give (exact and asymptotic) formulas for the growth rate of the length of the tensor powers when working over a good characteristic. As examples, we compute the growth rates for the full transformation monoid, the symmetric inverse monoid, and the monoid of 2 by 2 matrices. We also provide code used for our calculation.
What is the point?
Monoids are like groups with irreversible operations allowed. Their representation theory is richer and messier, but tensor powers still seem to follow computable growth laws. This paper proposes and proves such laws in a broad range of cases.
allow noninvertible symmetries.
use the group of units.
predict tensor-power decompositions.
More details
Let \( M \) be a finite monoid, and let \( k \) be a splitting field for \( M \) of characteristic \( p \ge 0 \). For a \( kM \)-module \( V \), we are interested in the quantity \[ b(n) = b^{M,V}(n) = \text{the number of \( M \)-indecomposable summands in } V^{\otimes n} \text{ (counted with multiplicity)}. \] In particular, we ask the following questions:
- Can we find a formula for \( b(n) \), or more generally a formula for an asymptotic expression \( a(n) \) with \( b(n) \sim a(n) \)? (Here \( b(n) \sim a(n) \) means that \( \frac{b(n)}{a(n)} \xrightarrow{ n \to \infty } 1 \).)
- Can we understand the rate of geometric convergence by quantifying how fast \( | \frac{b(n)}{a(n)} - 1 | \) converges to 0?
- Similarly, can we bound the variance \( | b(n) - a(n) | \)?
For example, we prove the conjecture under the hypothesis that some projective \( kG \)-module is injective as a \( kM \)-module. While the hypothesis is somewhat restrictive, it is satisfied by important classes of monoids such as the full transformation monoids \( T_n \) (in characteristic 0), the monoid of \( 2 \times 2 \) matrices \( M(2,q) \) (over defining characteristic), and all monoids with semisimple monoid algebra.
