Data
- Title: On Hecke and asymptotic categories for complex reflection groups
- Authors: Abel Lacabanne, Daniel Tubbenhauer and Pedro Vaz
- Status: To appear in Port. Math. Last update: Mon, 2 Sep 2024 07:28:44 UTC
- Code and (possibly empty) Erratum: Click
- ArXiv link: https://arxiv.org/abs/2409.01005
Abstract
Generalizing the dihedral picture for G(M,M,2), we construct Hecke algebras (and categories) and asymptotic counterparts. We think of these as associated with the complex reflection group G(M,M,N).
A few extra words
Weyl groups are among the most important objects in algebra, as they govern the representation theory of their associated reductive group.
Weyl groups are real reflection groups and special cases of complex reflection groups, and it is an interesting question what kind of ‘reductive group’ is
associated with a complex reflection group. These ‘reductive groups’ are believed to exist in a certain sense, and they were famously named
after the Greek island Spetses: such a ‘reductive group’ is called a spets.
We cannot provide a definitive answer to what spetses are, but recent developments indicate that Soergel bimodules, also known as
Hecke categories, can often serve as a replacement whenever an associated geometric or Lie theoretic picture is missing.
Thus, one might hope that Hecke categories could provide insights into what these spetses are.
In this paper, we focus on the complex reflection groups of type G(M,M,N) and suggest that they have an associated Hecke algebra and category. These arise from Chebyshev polynomials associated with root systems,
have Kazhdan–Lusztig (KL) type combinatorics, include asymptotic categories, are related to Calogero–Moser (CM) families, and encode Fourier matrices for G(M,M,N).
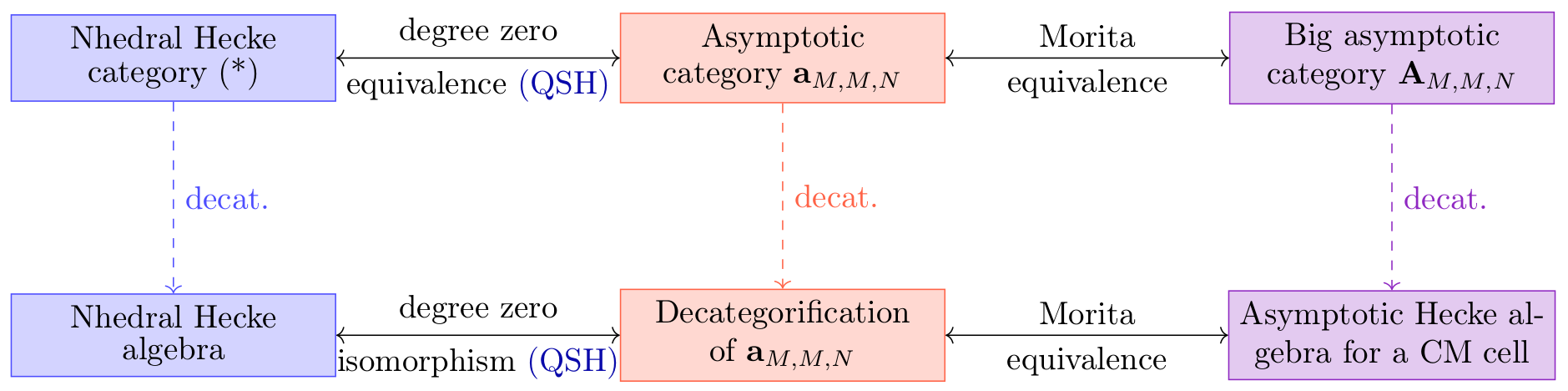
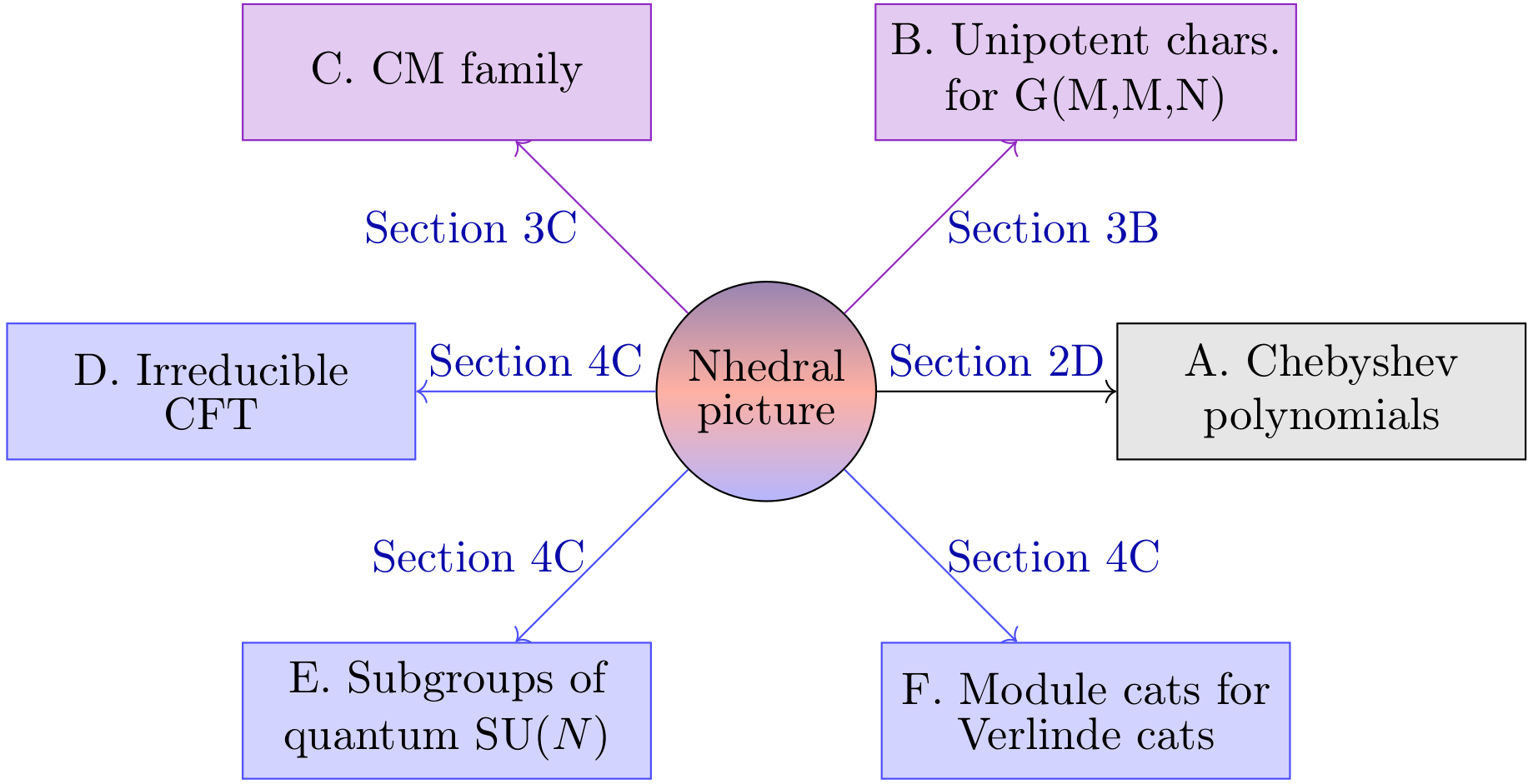
The following two diagrams illustrate our construction: