Research paper

Orthogonal webs and semisimplification

A diagrammatic category of orthogonal webs for tilting representations of orthogonal groups, including positive characteristic.

orthogonal groupswebstilting modulessemisimplification
arXiv

Data

  • Title: Orthogonal webs and semisimplification
  • Authors: Elijah Bodish and Daniel Tubbenhauer
  • Status: Comb. Theory 5 (2025), no. 3, Paper No. 12, 76 pp. Last update: Tue, 2 Sep 2025 19:03:23 EST
  • arXiv: https://arxiv.org/abs/2401.00704

Abstract

We define a diagrammatic category that is equivalent to tilting representations for the orthogonal group. Our construction works in characteristic not equal to two. We also describe the semisimplification of this category.

What is the point?

Webs replace linear algebra by pictures. This paper builds a web calculus for orthogonal groups and uses it to describe tilting representations and their semisimplification, including in prime characteristic away from two.

Pictures:
trivalent orthogonal webs.
Algebra:
tilting O_N-representations.
Application:
semisimplification.

More details

In this paper we define a diagrammatic category of orthogonal webs that is equivalent to tilting representations of the orthogonal group.
A closed orthogonal pre-web is a trivalent graph with edges labeled with integers \(\{1,\dots,N\}\) such that we have \(k\), \(l\) and \(k+l\) around every trivalent vertex. A closed orthogonal web is an immersion of a closed orthogonal pre-web such that each point of intersection is a crossing in the usual sense. As usual in diagrammatic algebra, cutting these graphs open and putting them into a strip with bottom and top boundary points gives a way to define morphisms, called orthogonal webs, in a monoidal category. The picture above shows two examples, the left one being closed.

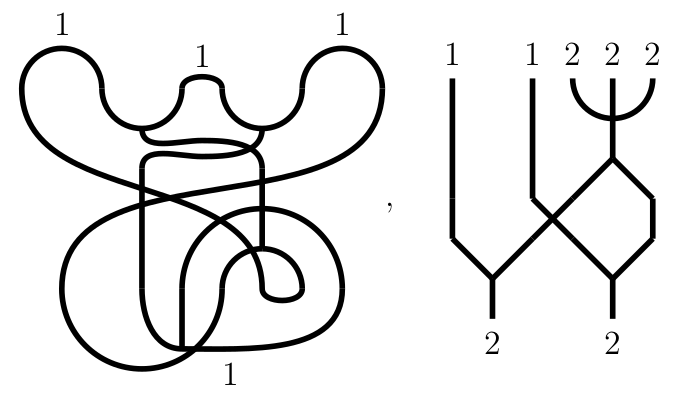
If in this or other illustrations an edge is not labeled, then its label is determined by other labels and we omitted it to avoid clutter.
Summarized, we:
  1. Fix \(p=0\) or any prime \(p\) not equal to \(2\). Let \(\mathbb{F}\) be an infinite field of characteristic \(p\) containing \(\sqrt{-1}\).
  2. We give a diagrammatic presentation of tilting \(O_{N}(\mathbb{F})\)-representations using orthogonal webs. This extends the result of Sartori to prime characteristic.
  3. A main ingredient is Howe's orthogonal duality in prime characteristic.
  4. As an application we describe the semisimplification of tilting \(O_{N}(\mathbb{F})\)-representations. Here \(p\neq 2\) is arbitrary and does not need to be bigger than \(N\).