Data
- Title: Relative cellular algebras
- Authors: Michael Ehrig and Daniel Tubbenhauer
- Status: Transform. Groups 26 (2021), no. 1, 229-277. Last update: Thu, 12 Sep 2019 08:38:59 UTC
- ArXiv link: https://arxiv.org/abs/1710.02851
- ArXiv version = 0.99 published version
Abstract
In this paper we generalize
cellular algebras by allowing
different partial orderings relative to
fixed idempotents. For these
relative cellular algebras we classify and construct simple modules, and
we obtain other characterizations in analogy to cellular algebras.
We also give several examples
of algebras that are relative cellular,
but not cellular. Most prominently, the restricted enveloping
algebra and the small quantum group for \(\mathfrak{sl}_{2}\), and an annular version of arc algebras.
A few extra words
In pioneering work Graham-Lehrer
introduced the notion of a cellular algebra, i.e.
an algebra equipped with a so-called cell datum.
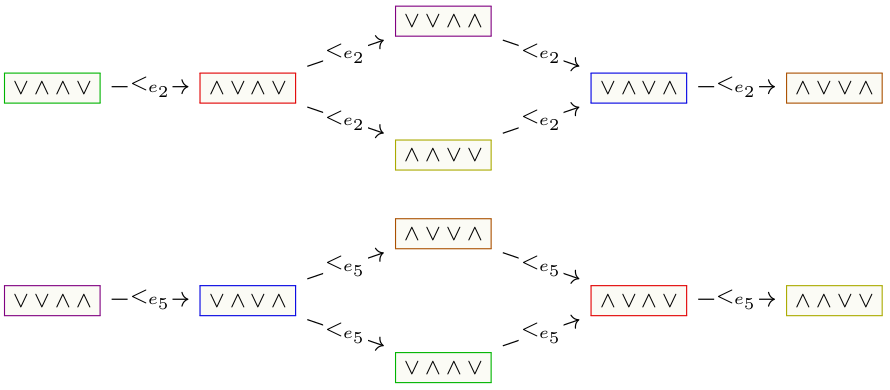
For example, of key importance for this paper, the cell datum
comes with a set \(\mathsf{X}\) and a partial order \(<\) on it.
The cell datum provides a method
to systematically reduce hard questions about the
representation theory of such algebras to problems in
linear algebra. Hereby the partial order \(<\) on \(\mathsf{X}\)
plays an important role since it yields an “upper triangular way”
to construct certain modules, called \textit{cell modules}, which
have a crucial role in the theory.
In well-behaved cases the linear algebra problems
can be solved giving e.g. a parametrization of
the isomorphism classes of simple modules
via a subset of \(\mathsf{X}\), and a construction
of a representative for each class.
In this paper we (strictly) generalize the
notion of a cellular algebra to what we call
a relative cellular algebra, i.e.
an algebra equipped with a relative cell datum.
For example, the relative cell datum
comes with a set \(\mathsf{X}\), but now with several partial
orders \(<_{\boldsymbol{\varepsilon}}\) on it, one for each idempotent \(\boldsymbol{\varepsilon}\)
from a preselected set of idempotents.
Taking only one idempotent \(\boldsymbol{\varepsilon}=1\), namely
the unit, and only one partial order \(<_{1}=<\), we recover the
setting of Graham-Lehrer.
Surprisingly, most of the theory of cellular algebras
still works in this relative setup. However, with
fairly different proofs, carefully incorporating the
various partial orders.
The purpose of our
paper is to explain this in detail.
One of our main examples of an algebra which is relative cellular,
but not cellular in the usual sense is an annular version
of arc algebras with the following picture to be kept in mind: