Data
- Title: Representation gaps of rigid planar diagram monoids
- Authors: Willow Stewart and Daniel Tubbenhauer
- Status: preprint. Last update: Fri, 9 May 2025 07:37:15 UTC
- Code and (possibly empty) Erratum: Click
- ArXiv link: https://arxiv.org/abs/2505.05846
Abstract
We define non-pivotal analogs of the Temperley–Lieb, Motzkin, and planar rook monoids, and compute bounds for the sizes of their nontrivial simple representations. From this, we assess the two types of monoids in their relative suitability for use in cryptography by comparing their representation gaps and gap ratios. We conclude that the non-pivotal monoids are generally worse for cryptographic purposes.
A few extra words
Noncommutative monoids are often vulnerable to linear attacks: an attacker can convert a protocol operating in such a
monoid into a linear algebra problem, enabling the use of powerful linear algebra techniques to break the encryption. Converting such a protocol to linear algebra requires a
nontrivial, say simple or faithful, representation of the monoid. In short, a cryptographic protocol based on a noncommutative monoid can be bypassed by targeting the nontrivial
simple representations, so if these are too low in dimension, the protocol will not be secure. The security of such a protocol can be roughly measured by the representation gap (RepGap) being the
dimension of the smallest nontrivial representation.
As such, it is important to find monoids with large RepGaps. There are also many other reasons to study these numerical invariants of monoids, including studying it for its own sake.
This paper begins the study of this with non-pivotal, rigid analogs of some of the classical planar diagram monoids,
namely the Temperley--Lieb monoid, Motzkin monoid, and the planar rook monoid. The rigid Temperley–Lieb category, as
we define it, has been studied as the free rigid monoidal category.
As far as we are aware, there is no existing definition for a rigid analog for the Motzkin monoid. Since the planar rook category
has no duals, we treat it as a two-color submonoid of the rigid Motzkin monoid.
One might assume that a more complicated monoidal category would translate to more secure cryptographic protocols; however, surprisingly,
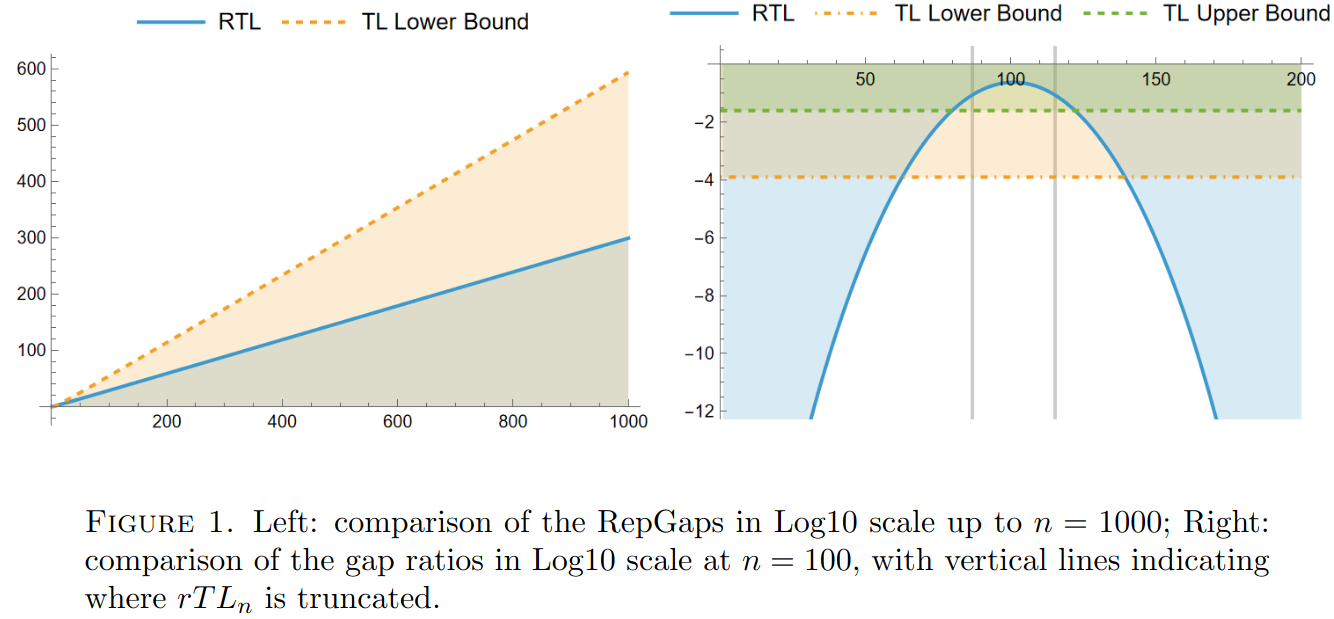
we find that the RepGap and gap ratio (=the RepGap normalized by the order of the monoid; we want this to drop to zero as slow as possible) are largely worse for the non-pivotal diagram monoids.
Here is one comparison: