My teaching philosophy

Let me explain my strategy to be a good teacher. My main pillars are:

Diversity

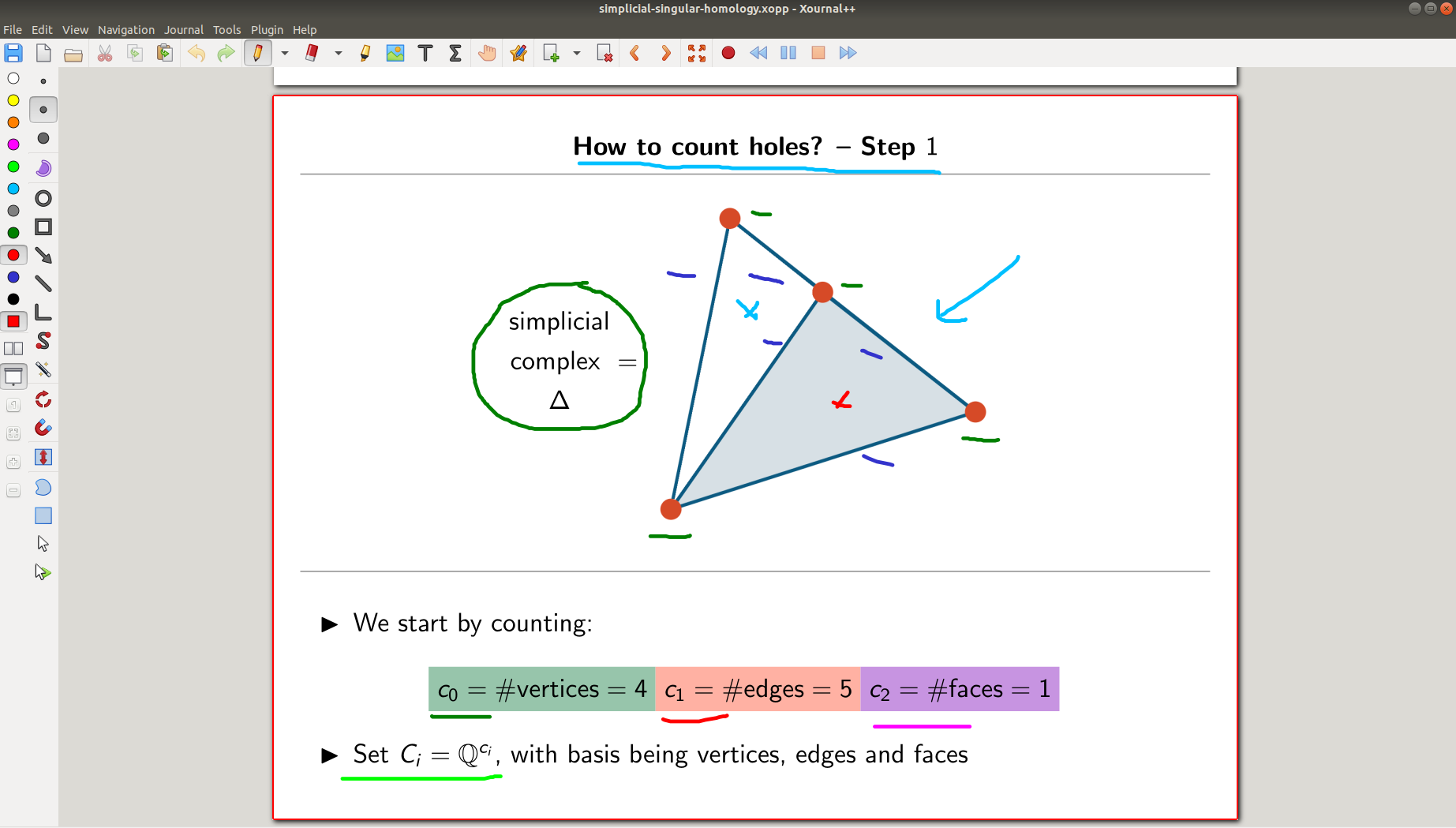
We all know that diversity is crucial for the progress of human societies. As part of such, diversity also plays a crucial role in teaching. The question what is the ``best'' or an ``appropriate'' form of (mathematical) education is indeed a hard question and no general answer is known. I believe that students learn best when they have access to a variety of pedagogical methods. This is where diversity comes into the game: we all learn the best when we are engaged in a variety of ways. To this end, I lecture, lead discussions, and allow my students to lecture and lead discussions, while also providing hands-on experiences. For example, when designing a lecture I usually choose a variety of presentation styles including face-to-face interactions via white/blackboard or beamer presentation, live streaming of the lecture, prerecorded YouTube videos and more. These all have their advantages and disadvantages, for example a prerecorded lecture can be watched anytime but is not very interactive. By varying my teaching method -- I sometime presentation slideshow, make a cartoon, record audio, or type on a document -- I try to ensure that diversity provides opportunities for all learners.
What I found most helpful for lectures is a mixture of prepared slides and live writing on screen (which I have done both, face-to-face and online). Here is an example from my class algebraic topology, explaining homology:

Authenticity

When working with students I strive to create authentic lessons. It is well-known in educational studies that students learn best when they are able to work through real-life, authentic scenarios. What real-life means in a lecture on abstract mathematics is a bit questionable. My approach is that I use a lot of computer-based animations: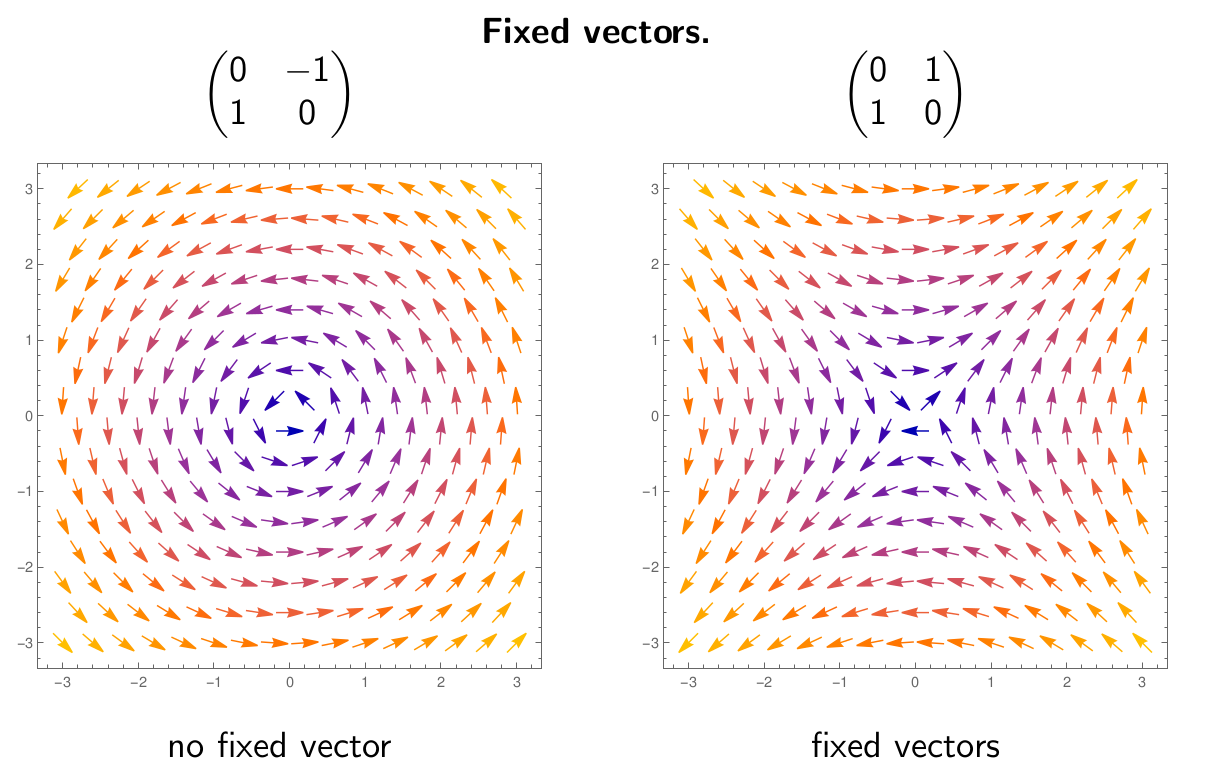 This is an example of me explaining the concept of eigenvectors: you can clearly seem them in the illustrations (or their absence in the left illustration) because they form ``lines''. Such computer illustrations make abstract concepts authentic and concrete. Sadly, these forms of illustration and learning are not explored enough, and I try to improve my lectures and seminar by including as many such diagrams as possible. I also encourage students to do the same, for example via exercises and in tutorials.
By providing authentic learning for my students they are able to develop transferable skills such as oral and verbal communication, problem solving, and critical thinking. This is the goal in the end: I try my best such that my teaching brings independent, critical, effective, and compassionate thinkers to society.

Experiential

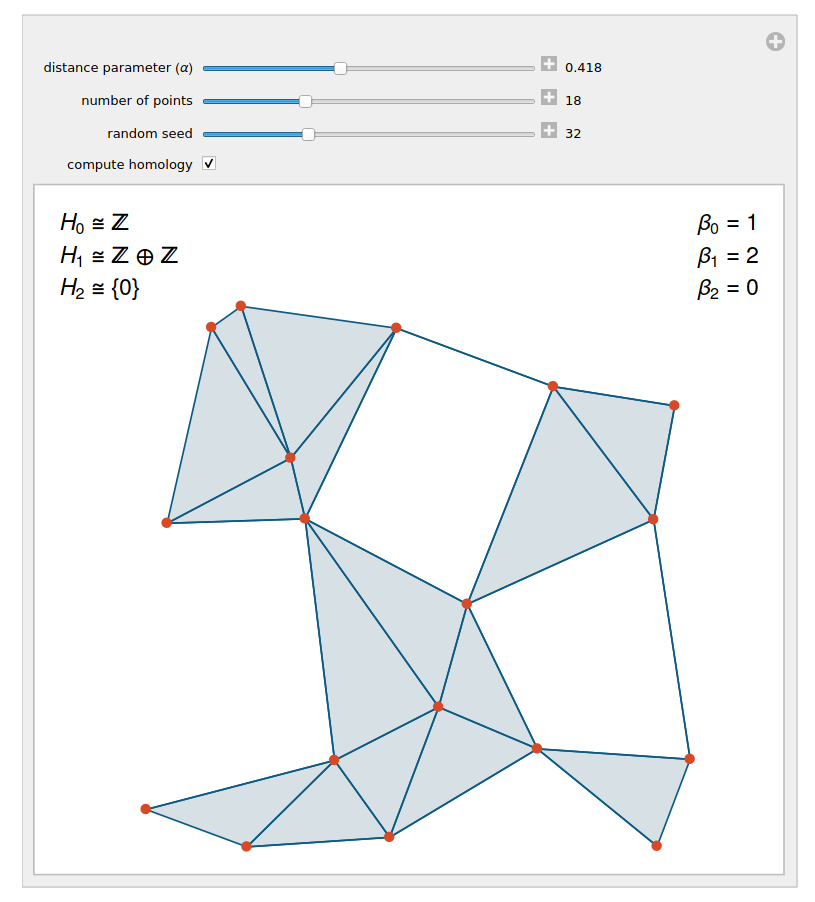
Most students learn best when they get hands-on experiences. Hands-on experiences are a bit hard to define, in particular in classes on abstract mathematics. Examples can include small or large group discussion by sharing their ideas or thoughts, creating or producing something, such as a video or website, and teaching other students a variety of skills or ideas.
A good way of doing this in my opinion is to have interactive websites and animations on various topics for various mathematical topics. Here is a screenshot of an interactive tool computing homology that I used for my aforementioned lecture on algebraic topology: This illustrates an example of persistent homology -- a nice application of the classical homology that the students appreciated very much. This way I provide opportunities for hands-on interactive lessons in my daily teaching, which also allows me an opportunity to provide both oral and written constructive feedback.

Inspirational

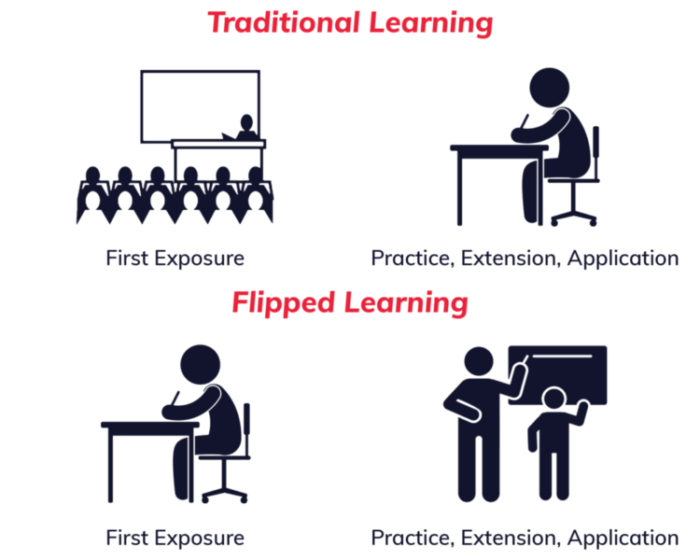
All of the above would be useless without enthusiasm. When I teach, I see it as my chance to share my knowledge and enthusiasm for research, teaching and learning. I am very passionate about research and education and want my students to become passionate as well. How can this be achieved?
On a personal level I inspire enthusiastic integration through active listening, humor, support, and actions that improve the learning environment. I encourage students to become designers of their own education. In practice, the keywords are flipped classroom: That is, the notion of a flipped classroom draws on concepts such as active learning, experiential learning, student engagement, hybrid course design and course podcasting. Think about students organizing their own tutorial classes. This gives students an opportunity to share their pre-existing knowledge and beliefs. As the students share their ideas, not only are they able to learn from their classmates, but I learn from them as well. Together, as I facilitate and guide them, my students are able to construct new knowledge that builds upon their previous knowledge. This concept of flipped classroom is already very present in seminars where students are the main players and I most keep on watching only directing and leading if necessary, including academic and social support.

Personal experience

All of my positions in the past were focused on research. But I always took the opportunity to give lectures, help to organize classes, exams and seminars, and advise students (several Ph.D., master and bachelor students). In fact, I gave lectures for quite diverse courses such as classes or seminars for Ph.D. or master students -- with only a small number of participants, but difficult topics -- and classes for beginners -- with hundreds of students, but rather easy mathematics. Indeed, it is a formidable, but worthwhile, challenge to teach such classes.
I already started quite early to get some teaching experience, since I took the opportunity as a young undergraduate student to teach as a Hilfswissenschaftler (undergraduate teaching assistant), helping to teach the classes I had attended before. I started teaching already in my second year as an undergraduate. While doing so, I realized in what sense the idea of using students to teach students has advantages and disadvantages. The main advantage is that the gap between students is not so big - compared to the gap between students and the professors or assistants - and therefore the younger students are not afraid to ask questions. The main disadvantage is that the older students do not have enough knowledge and experience yet.
Later, when I was a teaching assistant, I tried to avoid the main disadvantage, but, on the other hand, I tried to keep the main advantage by always staying in personal communication with the students. Since I got a lot of positive feedback from the students, I think I was successful. Moreover, I always liked teaching and I realized how useful it is even for my own personal development.
I never stopped following this path. Nowadays I give my own lectures -- most recently algebraic topology. I see it as my duty and pleasure to encourage and lead students by making the biggest possible effort to present the material in an accessible and enjoyable manner so that the students are willing and passionate to learn, ask questions and interact with me and their fellow students as well.

Goal

I acknowledge that I still have much to learn to be an effective educator. What drives me is my passion and love for mathematics, research and teaching. My ultimate goal is to teach the students to hone their skill in critical thinking and analytical reasoning. Although, of course, one has to teach them the technical parts too, I think one should always keep this goal in mind. Being a mathematician, I think it is in particular important to train students in three pillars: technical ability, interdisciplinary thinking, and creative problem solving.
Simply put, my ultimate goal is to train students to become mature and independent thinkers.