Data
- Title: A formula to evaluate type A webs and link polynomials
- Authors: Abel Lacabanne, Daniel Tubbenhauer and Pedro Vaz
- Status: Ark. Mat. 62 (2024), no. 1, 83-101. Last update: Mon, 3 Jun 2024 07:37:54 UTC
- ArXiv link: https://arxiv.org/abs/2209.12169
- ArXiv version = 0.99 published version
- Source: click
- GitHub for the code: click
Abstract
We give a closed formula to evaluate exterior webs (also called MOY webs) and the associated Reshetikhin-Turaev link polynomials.
A few extra words
This work in a combination of https://arxiv.org/abs/1404.5752 and
https://arxiv.org/abs/2108.05508.
The Reshetikhin-Turaev invariants of links are one of the most
important family of link invariants in quantum topology and its ramifications.
In this note we focus on the
subfamily of these invariants given by coloring the strands
of links with exterior powers of the vector representation of
quantum \(\mathfrak{sl}_n\) or quantum \(\mathfrak{gl}_n\). We show that this
family of polynomials can be computed by a \emph{closed formula}
that takes as input only combinatorial data associated to
a fixed colored link diagram and root theoretic data associated
to the type A Dynkin diagram. The formula works for all links, all coloring, and all ranks.
Let us stress that, by its very nature, the closed formula we give is
a Weyl-character-type formula: On the one hand,
it is general, completely algorithmic
and reveals abstract properties of the family of exterior colored link
polynomials. But on the other hand, the formula does not give an efficient way to compute these invariants, at least not without massaging it a bit.
The diagrammatic incarnation of this family of link invariants is
given by (exterior \(\mathfrak{sl}_n\) or \(\mathfrak{gl}_n\)) webs as shown in many
works.
In fact, the aforementioned formula is an application of
a closed evaluation formula for webs
that we will also state and prove.
This formula does not need any combinatorics on webs or tableaux;
it in fact does not even need the webs at all.
Moreover, another application of this formula
is an easy to check criterion for webs to represent dual canonical basis elements.
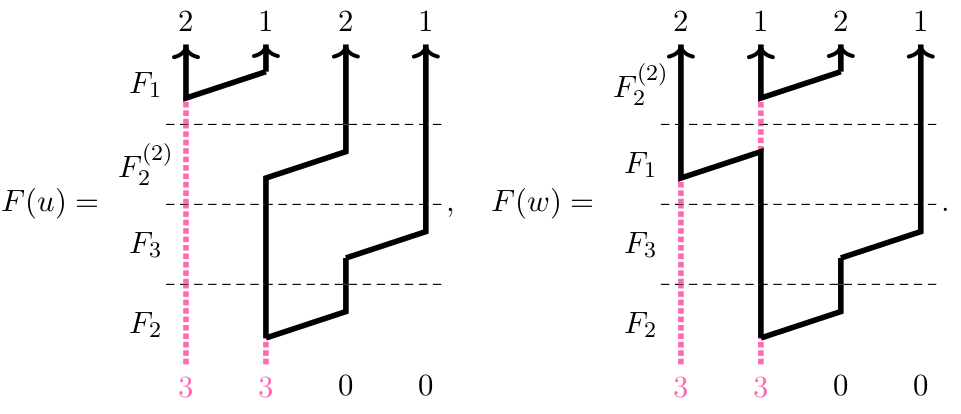
Here is an explicit example. First, bring the webs for which you want to calculate the evaluation into F-form (the choices how to do this does not affect the result):