Data
- Title: The \(\mathfrak{sl}_3\) web algebra
- Authors: Marco Mackaay, Weiwei Pan and Daniel Tubbenhauer
- Status: Math. Z. 277-1-2 (2014), 401-479. Last update: Sat, 10 Mar 2018 12:15:16 GMT
- ArXiv link: http://arxiv.org/abs/1206.2118
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1
Abstract
In this paper we use Kuperberg's \(\mathfrak{sl}_3\) webs and Khovanov's \(\mathfrak{sl}_3\) foams to define a new algebra \(K_S\), which we call the \(\mathfrak{sl}_3\) web algebra. It is the \(\mathfrak{sl}_3\) analogue of Khovanov's arc algebra \(H(n)\). We prove that \(K_S\) is a graded symmetric Frobenius algebra. Furthermore, we categorify an instance of quantum skew Howe duality, which allows us to prove that \(K_S\) is Morita equivalent to a certain, cyclotomic KLR-algebra. This allows us to determine the Grothendieck group of \(K_S\), to show that its center is isomorphic to the cohomology ring of a certain Spaltenstein variety, and to prove that \(K_S\) is a graded cellular algebra.
A few extra words
The main idea of the \(\mathfrak{sl}_3\) web algebra is simple, i.e. given four webs \(w_1,w_2,w_3\) and \(w_4\), which are the same at the boundary, one can define two new webs \(w_1w_2\) and \(w_3w_4\) by rotating \(w_1\) and \(w_3\) around the x-axis, s witching their orientation and glue them on top of \(w_2\) and \(w_4\). Then a multiplication \(m(f(w_1w_2),f(w_3w_4))\) of foams with the corresponding webs as boundary can be defined as follows:
- If \(w_2\) and \(w_3\) are different, then, by convention, the multiplication is zero.
- If \(w_2=w_3\), then glue the foams together via a multiplication foam.
- The multiplication foam is made of saddles (arc-split), unzips (Y-split) and square removals (H-split). The picture shows a saddle and an unzip.
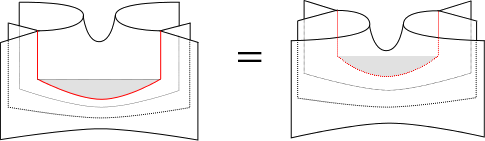
- The picture below is one part of the proof that the multiplication does not depend on the isotopy type. Note that the part of the foams corresponding to \(w_1\) and \(w_4\) is not shown, since it will be the identity.
- Note that one can speak of a categorification, i.e. on web level the multiplication is trivial (erase the middle and glue top and bottom), but on foam level lots of interesting mathematics is happening.