Data

  • Title: On rank one 2-representations of web categories
  • Authors: Daniel Tubbenhauer
  • Status: Algebr. Comb. Volume 7 (2024) no. 6, pp. 1813-1843. Last update: Tue, 10 Dec 2024 05:57:33 UTC
  • Code and (possibly empty) Erratum: GitHub
  • ArXiv link: https://arxiv.org/abs/2307.00785

Abstract

We classify rank one 2-representations of \(\mathrm{SL}_{2}\), \(\mathrm{GL}_{2}\) and \(\mathrm{SO}_{3}\) web categories. The classification is inspired by similar results about quantum groups, given by reducing the problem to the classification of bilinear and trilinear forms, and is formulated such that it can be adapted to other web categories.

A few extra words

The pictures to keep in mind while reading the below are the following, showing, in order, \(\mathrm{SL}_{2}\), \(\mathrm{GL}_{2}\) and \(\mathrm{SO}_{3}\) webs.
\(\mathrm{SL}_{2}\) webs, also known as Temperley-Lieb diagrams are:

\(\mathrm{GL}_{2}\) webs are:
The webs contain an oriented version of \(\mathrm{SL}_{2}\) webs, see above.
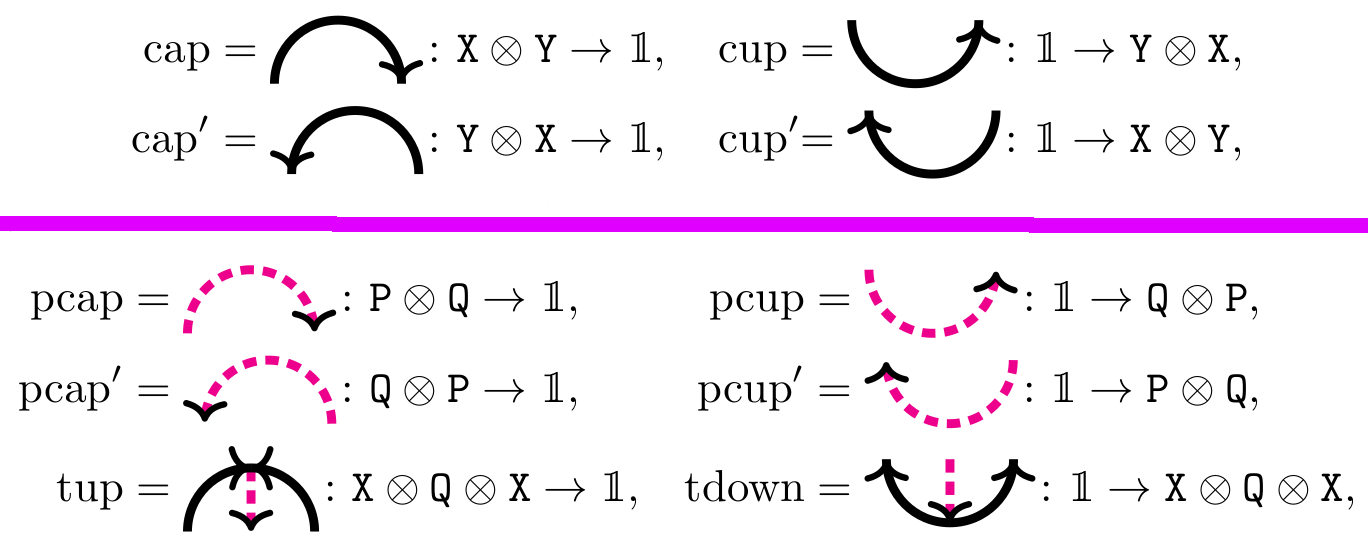
\(\mathrm{SO}_{3}\) webs are:
Classification is a central topic in all of mathematics. In representation theory the most important classification problem is to construct and compare all simple representations. In higher representation theory, an offspring of categorification that originates in several seminal papers, the most crucial classification problem is about the appropriate analog of simple representations. For example, given a favorite monoidal category, one can ask whether one can classify its simplest possible module categories. The favorite categories of our choice in this note are certain diagram categories, simplest possible will mean simple transitive and classification will mean reduction of the original problem to linear algebra.
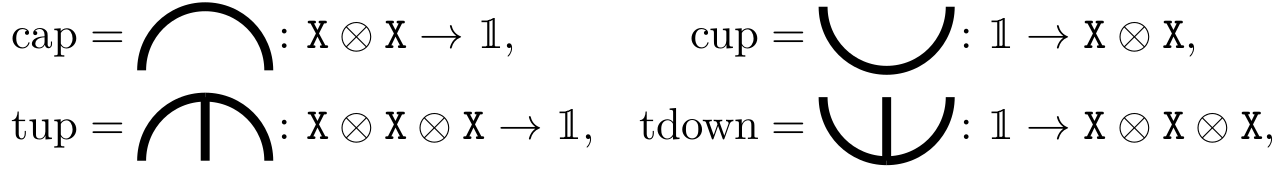
The problem of classifying symmetric and alternating bilinear forms is well-known and has a very pleasant answer. Less well-known but still doable and nice is the classification of all bilinear forms. On the other hand, the classification of trilinear forms seems tractable for small dimensions only, even if one restricts to symmetric or alternating forms. However, for small dimensions there is indeed a classification of trilinear forms.
In this note we will see a similar behavior for the three web categories above. The classification problem we have in mind for these categories is to study the easiest form of actions of these categories on finite dimensional complex vector spaces. That is, we want to classify rank one simple transitive 2-representations of these web categories.
We also analyze the complexity of the corresponding classification problems.