Finitary birepresentations of finitary bicategories
In this paper, we discuss the generalization of finitary 2-representation theory of finitary 2-categories to finitary birepresentation theory of finitary bicategories.
Data
- Title: Finitary birepresentations of finitary bicategories
- Authors: Marco Mackaay, Volodymyr Mazorchuk, Vanessa Miemietz, Daniel Tubbenhauer and Xiaoting Zhang
- Status: Forum Math. 33 (2021), no. 5, 1261-1320.
- arXiv link: https://arxiv.org/abs/2008.01658
- arXiv version = 0.99 published version
- LaTeX Beamer presentation: Slides 1, Slides 2, Slides 3, Slides 4, Slides 5, Slides 6, Slides 7
Abstract
In this paper, we discuss the generalization of finitary 2-representation theory of finitary 2-categories to finitary birepresentation theory of finitary bicategories. In previous papers on the subject, the classification of simple transitive 2-representations of a given 2-category was reduced to that for certain subquotients. These reduction results were all formulated as bijections between equivalence classes of 2-representations. In this paper, we generalize them to biequivalences between certain 2-categories of birepresentations. Furthermore, we prove an analog of the double centralizer theorem in finitary birepresentation theory.
What is the point?
In this paper, we discuss the generalization of finitary 2-representation theory of finitary 2-categories to finitary birepresentation theory of finitary bicategories.
A picture
A few extra words
Finitary 2-representation theory of finitary 2-categories is the categorical analog
of finite dimensional representation theory of finite dimensional algebras.
The main reason for restricting the framework to 2-representations of 2-categories,
was to avoid technical difficulties which naturally arise when one considers
birepresentations of bicategories in general: by weakening the axioms, the proofs of most results require more and bigger diagrams, whose commutativity is not always easy to show.
However, in the paper MMMTZ on the 2-representation theory of Soergel bimodules of finite Coxeter type,
it became clear that the 2-categorical setup is really too restrictive.
The main purpose of this paper is therefore to discuss the generalization of some important
foundational results on finitary 2-representation theory to finitary birepresentation theory. By discussing, we mean formulating those results carefully
in the greatest possible generality (or at least as generally as we currently can) and proving them in detail whenever the proof
is not straightforward and cannot be found in the literature.
A lot of the results in this paper will not surprise the experts, but we think that it is important to have the statements and their
proofs, which sometimes involve quite complicated diagrams, in written form somewhere in the
literature.
The picture above illustrates a change from the 2-categorical to the bicategorical setup: the adjunction (also called zigzag) relation now includes associators and unitors.
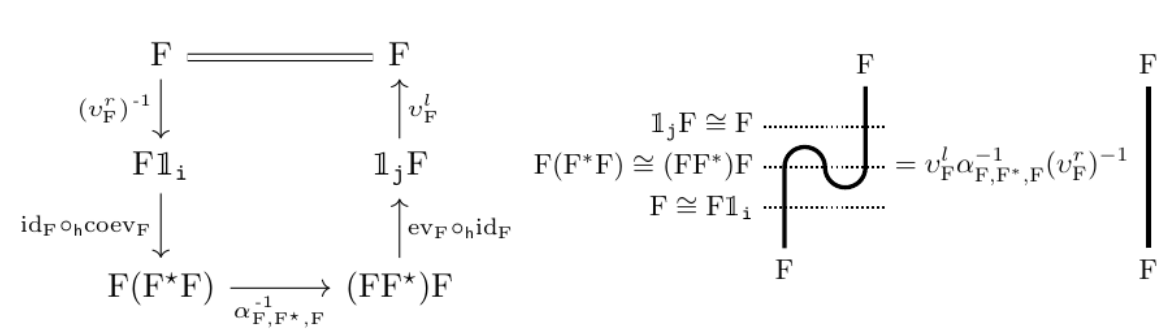
As a bonus, we prove a strong version of the \(\mathcal{H}\)-reduction theorem as well as a version of the double centralizer theorem
in our context, both of which are new.