Data

• Title: Generic $\mathfrak{gl}_{2}$-foams, web and arc algebras
• Authors: Michael Ehrig, Catharina Stroppel and Daniel Tubbenhauer
• Status: Preprint. Last update: Thu, 22 Oct 2020 14:24:54 UTC
• ArXiv link: http://arxiv.org/abs/1601.08010
• LaTex Beamer presentation: Slides1, Slides2

Abstract

We define parameter dependent $\mathfrak{gl}_{2}$-foams and their associated web and arc algebras and verify that they specialize to several known $\mathfrak{sl}_{2}$ or $\mathfrak{gl}_{2}$ constructions related to higher link and tangle invariants. Moreover, we show that all these specializations are equivalent, and we deduce several applications, e.g. for the associated link and tangle invariants, and their functoriality.

A few extra words

Let $\mathtt{Q}$ be a (certain) set of generic parameters. In this paper we introduce a $\mathtt{Q}$-version of singular topological quantum field theories (TQFTs) which we use to define a certain $\mathtt{Q}$-parameter foam $2$-category $\mathfrak{F}[\mathtt{Q}]$, that is a certain $2$-category of topological origin. We obtain from $\mathfrak{F}[\mathtt{Q}]$ several specializations. Among the specializations of this parameter version one can find the main foam $2$-categories studied in the context of higher link and tangle invariants:

• Khovanov/Bar-Natan's cobordisms
• Caprau's “foams”
• Clark-Morrison-Walker's disoriented cobordisms
• Blanchet's foams

A relation that holds for these parameter foams is the following: We also study the web algebra $\mathfrak{W}[\mathtt{Q}]$ corresponding to $\mathfrak{F}[\mathtt{Q}]$, i.e. an algebra which has an associated $2$-category of certain bimodules giving a (fully) faithful $2$-representation of $\mathfrak{F}[\mathtt{Q}]$. Similarly, we study also an algebraic model $\mathfrak{A}[\mathtt{Q}]$ called arc algebra.
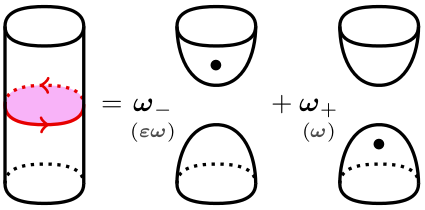
Our main result is, surprisingly, that any two specializations (under some conditions) are isomorphic/equivalent (our results are even stronger since everything is explicit). Similarly for the associated $2$-categories of bimodules and foams. This includes the four examples from above.
We discuss several applications of our explicit isomorphisms/equivalences. For example, we can show the higher tangle invariants constructed from the various $2$-categories are the same (they get identified by the above equivalence) and not just the associated link homologies.