Homepage Daniel Tubbenhauer - research paper gln webs

Data

Title: $\mathfrak{gl}_n$-webs, categorification and Khovanov-Rozansky homologies
Author: Daniel Tubbenhauer
Status: J. Knot Theory Ramifications 29-11 (2020), 96 pages. Last update: Fri, 2 Oct 2020 05:17:24 EST
ArXiv link: http://arxiv.org/abs/1404.5752
ArXiv version = 0.99 published version
LaTex Beamer presentation: Slides1, Slides2, Slides3

Abstract

In this paper we define an explicit basis for the $\mathfrak{gl}_n$-web algebra $H_n(\vec{k})$ (the $\mathfrak{gl}_n$ generalization of Khovanov's arc algebra) using categorified q-skew Howe duality.
Our construction is a $\mathfrak{gl}_n$-web version of Hu--Mathas' graded cellular basis and has two major applications: it gives rise to an explicit isomorphism between a certain idempotent truncation of a thick calculus cyclotomic KLR algebra and $H_n(\vec{k})$, and it gives an explicit graded cellular basis of the 2-hom space between two $\mathfrak{gl}_n$-webs. We use this to give a (in principle) computable version of colored Khovanov-Rozansky $\mathfrak{gl}_n$-link homology, obtained from a complex defined purely combinatorially via the (thick cyclotomic) KLR algebra and needs only F.

A few extra words

The main observation is that the $\mathfrak{gl}_n$-web space $W_n(\vec{k})$ is, under q-skew Howe duality, the $\dot{\textbf{U}}_q(\mathfrak{gl}_m)$-weight module of weight $\vec{k}$ in a certain $\dot{\textbf{U}}_q(\mathfrak{gl}_m)$-highest weight module.
It turns out that every $\mathfrak{gl}_n$-web can be obtained by a string of only F's acting as elements of $\dot{\textbf{U}}_q(\mathfrak{gl}_m)$ on a highest weight vector. Thus, we can say that the $\mathfrak{gl}_n$-web space $W_n(\vec{k})$ is an instance of $\dot{\textbf{U}}_q(\mathfrak{gl}_m)$-highest weight theory.
A closed $\mathfrak{gl}_n$-web is therefore nothing else than a quantum number since one jumps from the 1-dimensional highest weight space to the 1-dimensional lowest weight space using the F's of $\dot{\textbf{U}}_q(\mathfrak{gl}_m)$.
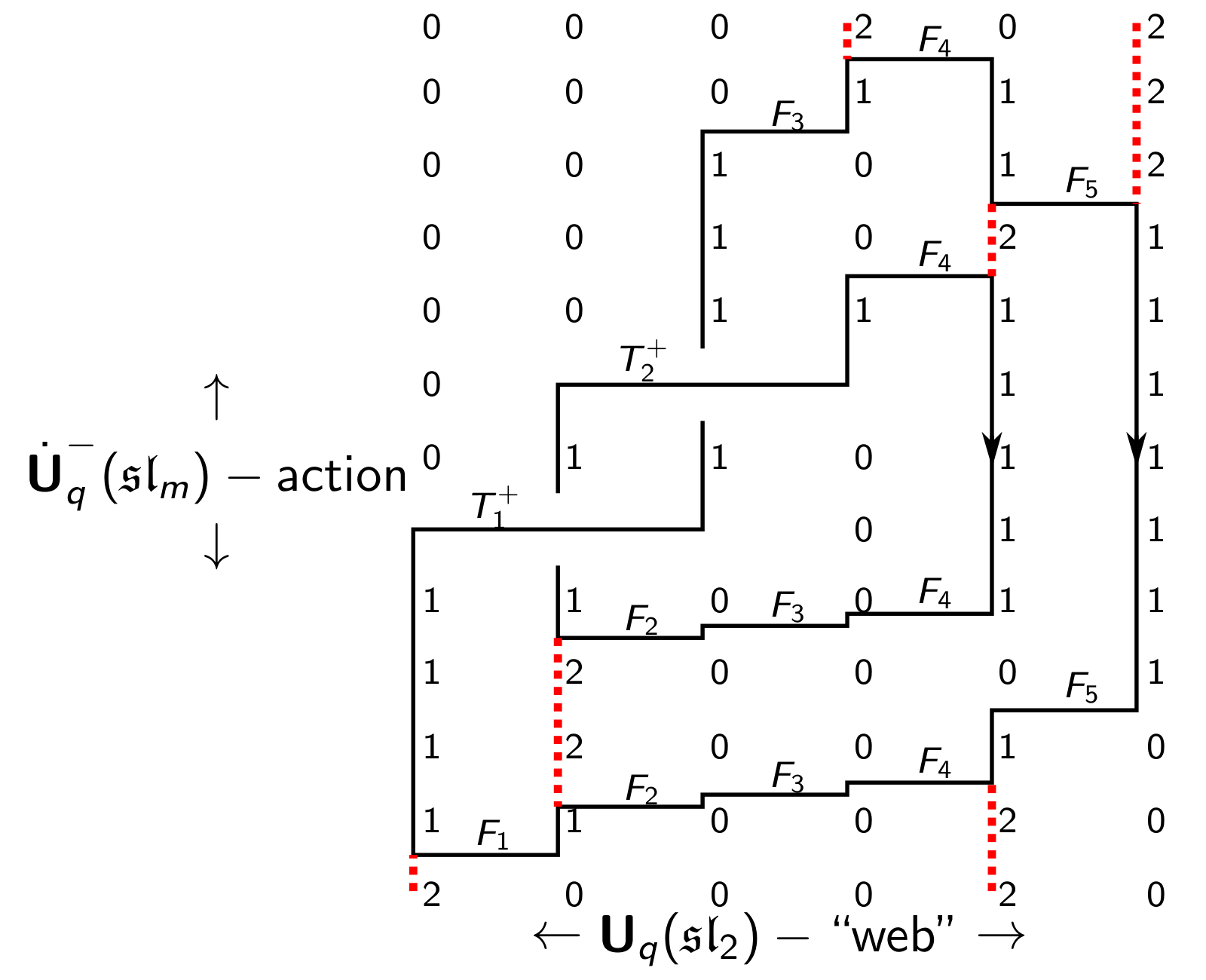
As a consequence: One can write each (colored) link as string of F's together with operators T for crossings. As for example displayed below for the Hopf link (with restriction to $n=2$). Here we act with the F's from bottom to top and the $\dot{\textbf{U}}_q(\mathfrak{gl}_m)$-weight spaces can be read of from the number grid.
The operators T measure the difference how one can hop around from the highest to the lowest weight and we obtain the Reshetikhin-Turaev $\mathfrak{gl}_n$-link polynomials therefore as an instance of $\dot{\textbf{U}}_q(\mathfrak{gl}_m)$-highest weight theory.
History repeats itself: The same is true for the $\mathfrak{gl}_n$-link homologies. We just replace the weight modules with weight categories, the F's with functors and the measurement of the difference with certain natural transformations.
And since everything an the level of the $\mathfrak{gl}_n$-link polynomials takes place in a certain $\dot{\textbf{U}}_q(\mathfrak{gl}_m)$-module of highest weight we can obtain the Khovanov-Rozansky $\mathfrak{gl}_n$-link homologies by only using the cyclotomic KL-R algebra.
Thus, these homologies are instances of categorified $\dot{\textbf{U}}_q(\mathfrak{gl}_m)$-highest weight theory.