Data
- Title: Trihedral Soergel bimodules
- Authors: Marco Mackaay, Volodymyr Mazorchuk, Vanessa Miemietz and Daniel Tubbenhauer
- Status: Fund. Math. 248 (2020), no. 3, 219-300. Last update: Wed, 19 Jun 2019 06:17:53 UTC
- ArXiv link: https://arxiv.org/abs/1804.08920
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1, Slides2 and Part II by Marco Mackaay: Slides, Slides3, Slides4, Slides5, Slides6
Abstract
The quantum Satake correspondence relates dihedral Soergel bimodules to the
semisimple quotient of the quantum \(\mathfrak{sl}_2\) representation category.
It also establishes a precise relation between the simple transitive
2-representations of both monoidal categories, which are indexed by bicolored
\(\mathsf{ADE}\) Dynkin diagrams.
Using the quantum Satake correspondence between affine \(\mathsf{A}_{2}\)
Soergel bimodules and the semisimple quotient of the quantum \(\mathfrak{sl}_3\)
representation category, we introduce trihedral Hecke algebras and Soergel
bimodules, generalizing dihedral Hecke algebras and Soergel bimodules. These
have their own Kazhdan-Lusztig combinatorics, simple transitive
2-representations corresponding to tricolored generalized \(\mathsf{ADE}\)
Dynkin diagrams.
A few extra words
In pioneering work, Kazhdan-Lusztig defined
their celebrated bases of Hecke algebras. Crucially, on these bases the structure
constants of the algebras belong to
\(\mathbb{N}_0=\mathbb{Z}_{\geq 0}\). This started a
program to study \(\mathbb{N}_0\)-algebras,
which have a fixed basis with non-negative
integral structure constants.
For these algebras it makes sense to study and classify
\(\mathbb{N}_0\)-representations, i.e. representations with a fixed basis on which the
fixed bases elements of the algebra act
by non-negative integral matrices. As it turns out,
\(\mathbb{N}_0\)-representations are interesting from various
points of view, with applications and connections to e.g. graph theory,
conformal field theory, modular tensor categories and subfactor theory.
The categorical incarnation of
\(\mathbb{N}_0\)-representation theory is 2-representation theory,
with simple transitive 2-representations playing the role of the simple
representations.
In this paper, we restrict our attention
to certain algebras
which we call trihedral Hecke algebras,
generalizing dihedral Hecke algebras, and their categorification by
trihedral Soergel bimodules, generalizing dihedral Soergel bimodules.
The analogy of the trihedral to the dihedral case is as follows, where we always
exclude the (trivial) cases of \(\mathbb{N}_0\)-representations or 2-representations of
rank one:
| Dihedral | Trihedral |
|---|---|
| The dihedral Hecke algebra is a quotient of the affine type \(\mathsf{A}_1\) Hecke algebra. | The trihedral Hecke algebra is a subquotient of the affine type \(\mathsf{A}_2\) Hecke algebra. |
| All simple representations are two dimensional. | All simple representations are three dimensional. |
| All simple representations can be constructed by using the roots of the Chebyshev polynomials. | All simple representations can be constructed by using the roots of Koornwinder's two variable version of the Chebyshev polynomials. |
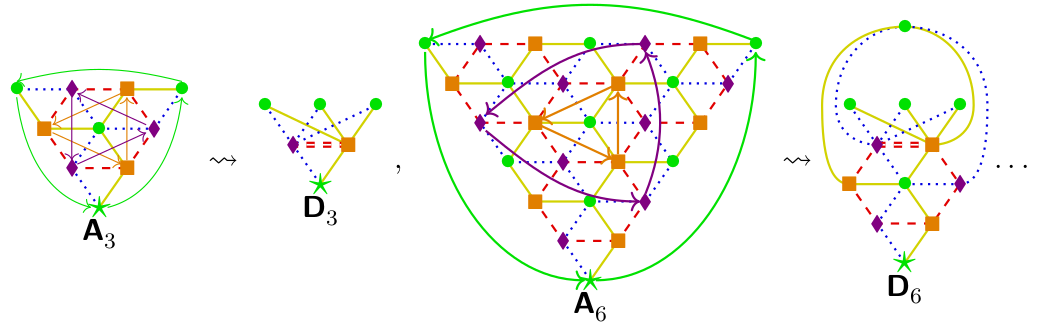
| The \(\mathbb{N}_0\)-representations are given by bicolored \(\mathsf{ADE}\) Dynkin diagrams. | The \(\mathbb{N}_0\)-representations should be classified by tricolored generalized \(\mathsf{ADE}\) Dynkin diagrams. |
| The simple transitive 2-representations are classified by bicolored \(\mathsf{ADE}\) Dynkin diagrams. | The simple transitive 2-representations should be classified by tricolored generalized \(\mathsf{ADE}\) Dynkin diagrams. |
| The quiver algebras underlying the simple transitive 2-representations of rank greater than one are the zigzag algebras of the corresponding Dynkin type. | The quiver algebras underlying the simple transitive 2-representations of rank greater than one should be analogs zigzag algebras of the corresponding generalized Dynkin type. |