Data

• Title: Khovanov homology for virtual tangles and applications
• Author: Daniel Tubbenhauer
• Status: Joint now with Virtual Khovanov homology using cobordisms, J. Knot Theory Ramifications 23-9 (2014), 91 pages. Last update: Sun, 2 Dec 2012 04:52:30 GMT
• ArXiv link: http://arxiv.org/abs/1212.0185.
• ArXiv version (this one: click)= 0.99 published version
• Poster: Poster

Abstract

We extend the cobordism based categorification of the virtual Jones polynomial to virtual tangles. This extension is combinatorial and has semi-local properties. We use the semi-local property to prove an applications, i.e. we give a discussion of Lees degeneration of virtual homology.

A few extra words

We admit right away that one main application of the construction is still missing, i.e. a computer program that uses the semi-local properties in the sense of Bar-Natans “divide and conquer” algorithm to perform bigger computations.
Nevertheless, we give two different extensions of the Khovanov homology for tangles in the virtual case. The main problem is that a straightforward extension is not possible in a nice way, since an open saddle can close of as three different surfaces, i.e. a multiplication, a comultiplication or even a Möbius cobordism.
Note that, if we assume that the characteristic of the underlying ring is not two, the latter one is zero. The problem that arises is, in order to maintain that the complex is a well-defined chain complex, one has to define some open saddles to be zero. But, after “tensoring” local pieces together, the corresponding saddles could be non-zero anymore. Hence, to solve this problem, we introduce another piece of data which we call indicator. This indicator is a number that is either +1,-1 or 0.
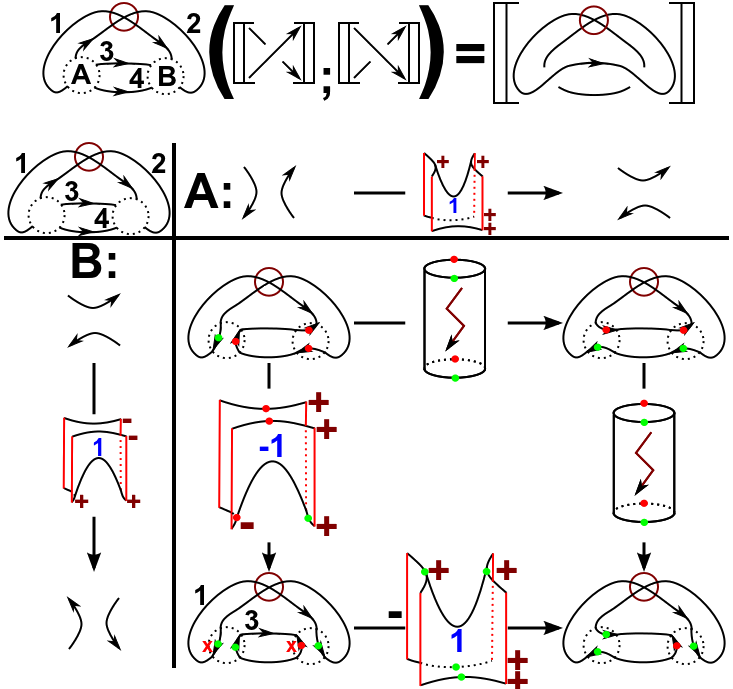
In order to use the local construction in a global picture, we introduce a specific way of calculation that we call dot-calculus. See in the picture below.
As an application of the whole progress we show that Lee's variant of a virtual knot is trivial which is the first input one needs if one want to define a virtual Rasmussen invariant.
A main tool to prove that the virtual Khovanov homology of a virtual knot is trivial, we prove that the two generators of the homology are precisely given by so-called non-alternating resolutions (as an example see the upper right resolution in the picture below) and that a virtual knot has exactly two of these resolutions. This is a completely combinatorial observation that tells us something about the combinatorial nature of a virtual knot.