Data

• Title: \(\mathrm{SL}_{2}\) tilting modules in the mixed case
• Authors: Louise Sutton, Daniel Tubbenhauer, Paul Wedrich and Jieru Zhu
• Status: Selecta Math. (N.S.) 29 (2023), no. 3, 39. Last update: Mon, 17 May 2021 10:52:03 UTC
• ArXiv link: https://arxiv.org/abs/2105.07724
• ArXiv version = 0.99 published version (will be updated soon)
• LaTex Beamer presentation: Slides, Slides2, Slides3, Slides4

Abstract

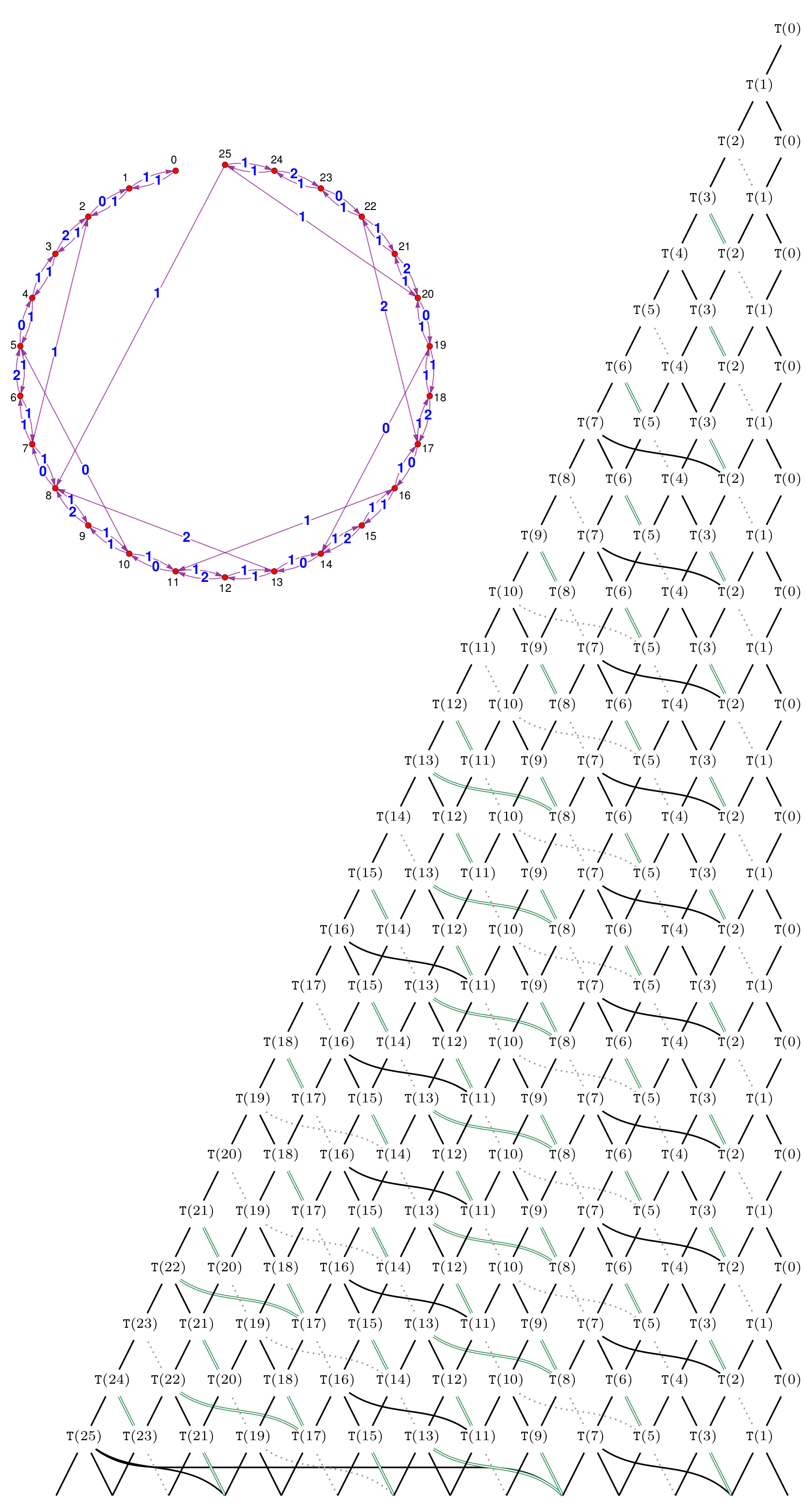
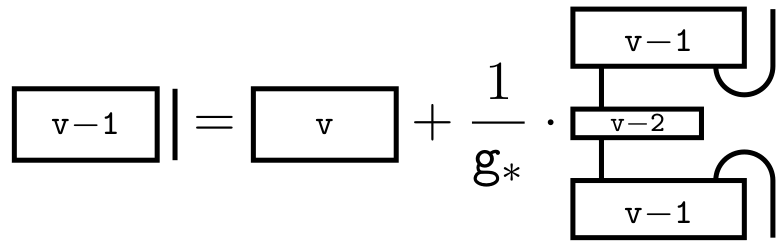
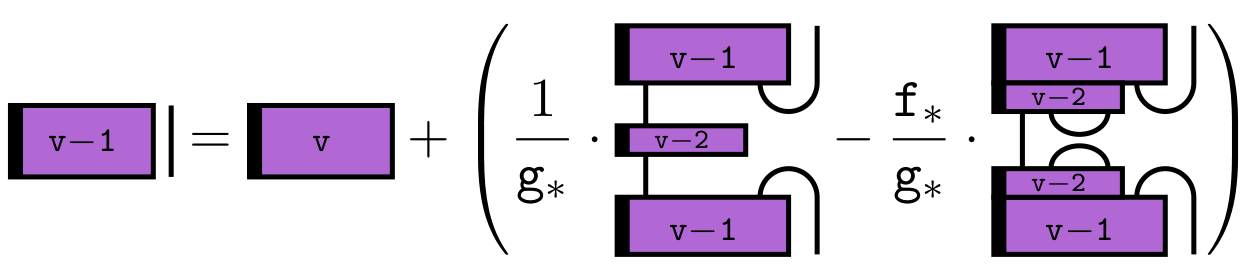
Using the non-semisimple Temperley-Lieb calculus, we study the additive and monoidal structure of the category of tilting modules for \(\mathrm{SL}_{2}\) in the mixed case. This simultaneously generalizes the semisimple situation, the case of the complex quantum group at a root of unity, and the algebraic group case in positive characteristic. We describe character formulas and give a presentation of the category of tilting modules as an additive category via a quiver with relations. Turning to the monoidal structure, we describe fusion rules and obtain an explicit recursive description of the appropriate analog of Jones-Wenzl projectors. We also discuss certain theta values, the tensor ideals, mixed Verlinde quotients and the non-degeneracy of the braiding.

A few extra words

In this paper we study categories of representations of \(\mathrm{SL}_{2}(\mathbb{K})\), or its associated quantum group quantized by using an invertible variable q, in the so-called mixed case or mixed characteristic. This can be thought of as the culmination of the following cases:

• The semisimple case where \(\mathbb{K}\) is for example the field of complex numbers.
• The complex quantum group case (at a root of unity) where \(\mathbb{K}\) is a field containing the complex numbers, one works with the quantum group and q is a root of unity in \(\mathbb{K}\).
• Characteristic p where \(\mathbb{K}\) is for example an algebraically closed field of prime characteristic.
• The “everything else” case, where one works with the quantum group, q is a root of unity in \(\mathbb{K}\), and \(\mathbb{K}\) is of prime characteristic.

The latter is an exciting case because of it fractal-type representation theory, a property that it shares with the prime characteristic case, and because it has a non-trivial braiding, a property that it shares with the complex quantum group case. The first aim of this paper is to give an overview of the state of the arts regarding \(\mathrm{SL}_{2}(\mathbb{K})\) in the mixed case, and, at the same time, to put an eye on the categorical properties of the representation categories. In particular, we recall/deduce some character formulas and generalize the main result of click to mixed characteristic. Our second aim, and maybe the real meat, is to study the representation categories associated to \(\mathrm{SL}_{2}(\mathbb{K})\) as (braided) monoidal categories, namely the fusion rules. Classically, fusion rules express the structure constants for the representation ring such into indecomposable modules. Here is an example of such a fusion graph (the fusion graph of tensoring with the vector representation) On the categorified level one is interested in explicitly describing the projection and inclusion maps realizing such decompositions. In the Temperley-Lieb context this means decomposing the tensor products into idempotents that project onto the indecomposable summands predicted by the fusion rule. A famous example is the recursion for the classical Jones--Wenzl projectors We establish decompositions analogous to this recursion in the mixed setting. As an example, we show an instance going beyond the Jones-Wenzl recursion with summands that need not be simple (here we use colored boxes to encode projectors corresponding to modules that need not be simple): We also study analogs of Kauffman-Lins type formulas, tensor ideals, Verlinde quotients, modified traces and the Müger center.