Data
- Title: Growth rates of the number of indecomposable summands in tensor powers
- Authors: Kevin Coulembier, Victor Ostrik and Daniel Tubbenhauer
- Status: Algebr. Represent. Theory 27 (2024), no. 2, 1033-1062. Last update: Wed, 10 Jan 2024 02:25:36 UTC
- ArXiv link: https://arxiv.org/abs/2301.00885
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1, Slides2, Slides3
Abstract
In this paper we study the asymptotic behavior of the number of summands in tensor products of finite dimensional representations of affine (semi)group (super)schemes and related objects.
A few extra words
A central, yet hard, problem in representation theory is the decomposition of tensor products of
representations into indecomposable summands. Computations of these decomposition numbers are often major unsolved problems in representation theory.
In this paper we take a different perspective and we are interested in asymptotic properties of
the number of indecomposables in tensor products
of representation rather than explicit decompositions. In contrast to
the question of explicit decompositions, we obtain results in extensive generality.
To get started, let \(\Gamma\) be an affine semigroup superscheme
(e.g. a group, a monoid or even a semigroup, including super versions; we actually have several other versions; see the paper for details)
with a finite dimensional representation \(V\) over some field (any field is allowed).
We let \(\beta^{\Gamma,V}:=\lim_{n\to\infty}\sqrt[n]{b_{n}^{\Gamma,V}}\) where
\(b_{n}^{\Gamma,V}\) denotes the number of indecomposable summands in \(V^{\otimes n}\).
Our main result is that, even in this generality, we can say something about this limit. Namely:
\(\beta^{\Gamma,V}=\dim V\).
Let us give an explicit example. Take the complex numbers as the ground field,
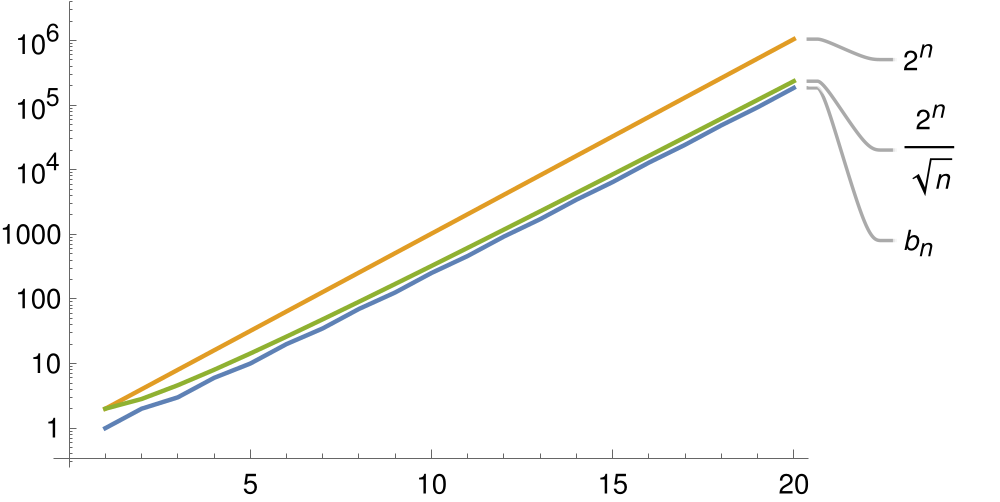
\(\Gamma_{2}=SL_{2}\) and \(V_{2}=\mathbb{C}^{2}\), its vector representation. Then the first numbers \(b_{n}^{\Gamma_{2},V_{2}}\) are:
\(\{1,1,2,3,6,10,20,35,70,126,252\},\quad b_{n}=b_{n}^{\Gamma_{2},V_{2}}\text{ for }n=0,\dots,10.\)
A Mathematica loglog plot of \(\sqrt[n]{b_{n}}\) (y-axis) for \(n\in\{1,\dots,1000\}\) (x-axis) gives

However, the asymptotic growth rate of \(b_{n}\) is slower than \(2^{n}\). Namely, it is essentially \(2^{n}/\sqrt{n}\) (the square root vanishes while taking the nth root, so we cannot see this in the main theorem):