“Lecture Representation theory”

What?

Symmetry is everywhere, and nature is designed symmetrically: Snails make their shells, spiders design their webs, and bees build hexagonal honeycombs, all based on the concept of symmetry. Indeed, symmetry is a general principle, which plays an important role in various areas of knowledge and perception, ranging from arts and aesthetics to natural sciences and mathematics. Representation theory is the systematic study of linear actions: in representation theory general symmetries are represented by matrices and one has now the whole power of linear algebra at hand to study symmetries. For example, the symmetry of a molecule influence its chemical properties.

This picture displays a two-fold symmetry \(s_{2}\) and a three-fold symmetry \(s_{3}\) of two molecules. How to study symmetries of molecules systematically? You guessed it: (also) via representation theory! The symmetries \(s_{2}\) and \(s_{3}\) can be modeled by rotation matrices, and the molecules by vector spaces. The matrices now act on the vector space associated to the molecules (this is called a linear action), and this is the approach representation uses. Representation theory, being the abstract study of the possible types of symmetry, is a fundamental area of algebra with applications throughout the sciences (not just chemistry as above): the methods of representation theory lead to conceptual and practical simplification of any problem in linear algebra where symmetry is present. 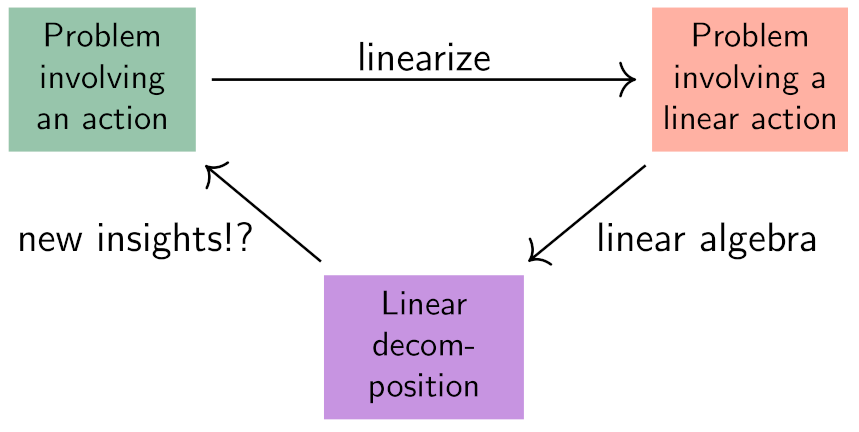The mnemonic is:

Let us zoom in a little bit. The study of group actions is of critical importance in mathematics and related fields such as physics and chemistry. Its significance can hardly be overestimated. The approach of Frobenius \(\sim\)1895, Burnside \(\sim\)1900 and many others, nowadays called representation theory, is to linearly approximate such actions. For example, let G be a group or a ring or an algebra etc. 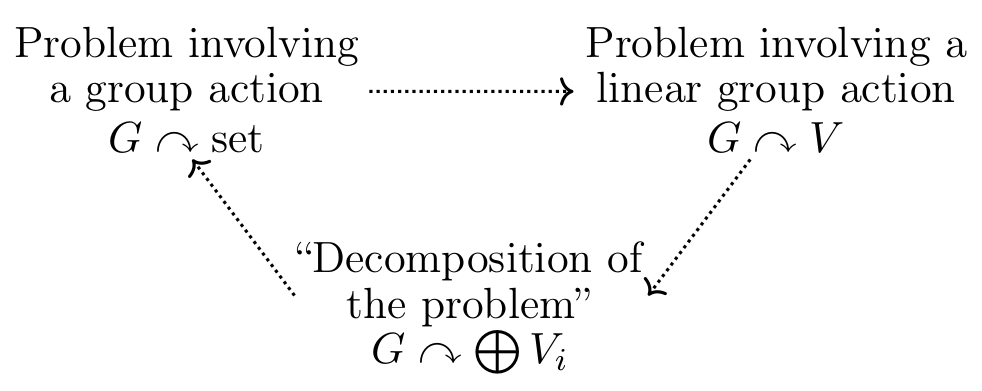Representation theory is the study of linear group actions \(G\longrightarrow\mathrm{E}\mathrm{nd}(V),\; g\mapsto M(g)\quad\text{or}\quad G\curvearrowright V\). That is, representation theory assigns to each group element a matrix M(g) acting on a vector space V -- its linear shadow. The representation theory approach is that classifying linear G-actions has, in contrast to arbitrary group actions, a satisfactory answer for many groups. The basic building blocks V\({}_{i}\) of such actions tell us a lot about the problem we started with. (The strategy of representation theorists is summarized below.) In fact, experience tells us that the collection of such linear shadows is an interesting structure in its own right and maybe even more worthwhile to study than G itself.

Developing over the past century (and still in development), Frobenius and Burnside's theory is pervasive across many fields of mathematics. The success of representation theory has led to numerous generalizations and applications, e.g. in the aforementioned molecular chemistry or quantum physics, but also in engineering such as robotics. (How do you figure out how robots move before building them? Indeed, using representation theory.) Still doubting the usefulness of representation theory? Well, Burnside did so as well. Here is a text from the introduction of Burnside's famous book Theory of groups of finite order. The top picture is from the original edition and the second picture from the revision. Can you spot how Burnside changed their mind?

(Linear substitutions is the old name for representations.)

Contact

Daniel Tubbenhauer email

Please put [Lecture Representation theory] as the subject.

Who?

Fourth semester students in Mathematics interested in a mixture of (linear) algebra and discrete mathematics, but everyone is welcome

Where and when?

The lecture.
- Every Monday from 12:00-14:00
- Online
Tutorials.
- Every Friday from 12:00-14:00
- Online
Material for the lecture.
- The lecture is a mix of various sources for group and monoid representations. The main source is [St12] for group representations and then [St16] for the monoid case, and the lecture follows the list of topics presented therein. The lecture sometimes takes a different perspective and potentially reading either of the classical references [CR62], [FH91] or [Se77] should be beneficial. [Be98] is a bit more abstract, but also a classic. Newer references are for example |Cr19], [E+11] (freely available), |Sa01] (for symmetric groups). These are also used for the lecture.
- Prerecorded lectures on the “What is...representation theory?” playlist here: Click
Summary: Click
Mini presentation: Click
The detailed plan: Click

Schedule

Speaker: Daniel Tubbenhauer, Topic: The beginnings - What is...representation theory?
Speaker: Daniel Tubbenhauer, Topic: Simple and indecomposable representations I - The elements
Speaker: Daniel Tubbenhauer, Topic: Simple and indecomposable representations II - More about elements
Speaker: Daniel Tubbenhauer, Topic: Characters I - The main players of representation theory!?
Speaker: Daniel Tubbenhauer, Topic: Characters II - Schur's orthogonality relations
Speaker: Daniel Tubbenhauer, Topic: Characters III - Abelian groups and Fourier analysis
Speaker: Daniel Tubbenhauer, Topic: Burnside's theorem - An application
Speaker: Daniel Tubbenhauer, Topic: Induction and restriction - The classical adjoint pair
Speaker: Daniel Tubbenhauer, Topic: Representations of symmetric groups - Young diagrams and co
Speaker: Daniel Tubbenhauer, Topic: Monoids I - Green's relations and friends
Speaker: Daniel Tubbenhauer, Topic: Monoids II - The Clifford-Munn-Ponizovskii theorem
Speaker: Daniel Tubbenhauer, Topic: Whats next? - Outlook

Exercises

The exercises correspond 1:1 to the talks in the list above.

Exercise 1, Click
Exercise 2, Click
Exercise 3, Click
Exercise 4, Click
Exercise 5, Click
Exercise 6, Click
Exercise 7, Click
Exercise 8, Click
Exercise 9, Click
Exercise 10, Click
Exercise 11, Click
Exercise 12, Click

References

Here are a few references used in this lecture:

[Be98] D.J. Benson. Representations and cohomology. I. Basic representation theory of finite groups and associative algebras. Second edition. Cambridge Studies in Advanced Mathematics, 30. Cambridge University Press, Cambridge, 1998. xii+246 pp.
|Cr19] D.A. Craven. Representation theory of finite groups: a guidebook. Universitext. Springer, Cham, 2019. viii+294 pp.
[CR62] C.W. Curtis, I. Reiner. Representation theory of finite groups and associative algebras. Reprint of the 1962 original. AMS Chelsea Publishing, Providence, RI, 2006. xiv+689 pp.
[E+11] P. Etingof, O. Golberg, S. Hensel, T. Liu, A. Schwendner, D. Vaintrob, E. Yudovina. Introduction to representation theory. With historical interludes by Slava Gerovitch. Student Mathematical Library, 59. American Mathematical Society, Providence, RI, 2011. viii+228 pp. https://math.mit.edu/~etingof/replect.pdf
[FH91] W. Fulton, J. Harris. Representation theory. A first course. Graduate Texts in Mathematics, 129. Readings in Mathematics. Springer-Verlag, \newblock New York, 1991. {\rm xvi}+551 pp.
|Sa01] B.E. Sagan. The symmetric group. Representations, combinatorial algorithms, and symmetric functions. Second edition. Graduate Texts in Mathematics, 203. Springer-Verlag, New York, 2001. xvi+238 pp.
[Se77] J.P. Serre. Linear representations of finite groups. Translated from the second French edition by Leonard L. Scott. Graduate Texts in Mathematics, Vol. 42. Springer-Verlag, New York-Heidelberg, 1977. {\rm x}+170 pp.
[St12] B.Steinberg. Representation theory of finite groups. An introductory approach. Universitext. Springer, New York, 2012. xiv+157 pp.
[St16] B. Steinberg. Representation theory of finite monoids. Universitext. Springer, Cham, 2016. xxiv+317 pp.