This page is speculative. If you are not up for rather unfinished ideas, then jump back by clicking on one of the pictures below. For a fantastic blog of an expert from which parts of this side are shamefully stolen click here.
High frequencies and representations of cyclic groups
Let us identify the representation theory of cyclic groups \(C_n=\mathbb{Z}/n\mathbb{Z}\) and wave functions. This is of course a bit of a shaky
identification, but if one thinks about the concept of e.g. periods of waves maybe not so far away from the truth.
In any case, this analogy will do its job for this page.
Consider now the most basic wave - the sine function. Its Fourier series is trivial, namely the function itself.
This is in some sense what happens to \(C_n\)-equivariant linear
maps in representation theory.
\(C_n\)-equivariant piecewise linear maps behave more like the following. Instead of the sine function consider
its composition with ReLU. (Recall that ReLU is \(\max(a,0)\)). The Fourier series gets much more exciting, try yourself:
In the above illustration one sees the appearance of higher and higher frequencies. Eventually these high frequencies
will dominant the whole picture.
In our analogy the high frequencies correspond to \(C_n\)-representations
that have less symmetry, so appear for small subgroups. In particular, the highest frequency corresponds to the
trivial \(C_n\)-representation.
Recall from here that this is exactly the picture we get
for the interaction graphs: the low frequencies \(\Leftrightarrow\) \(C_n\)-representations of high order
point towards the high frequencies \(\Leftrightarrow\) \(C_n\)-representations of low order.
Why is that important? Well, assume that we want to Artin–Wedderburn decompose ReLU. Then the picture is:

What we see here is that for ReLU itself there are 2 ingoing paths into the \(L_0\), the trivial \(C_3\)-representation, and one such paths for the other \(C_3\)-representation. In the second step we have 3 versus 1, and eventually the number of paths ending at \(L_0\) will explode. So the whole complexity of evaluating large powers of ReLU is dominated by \(L_0\), or, in our analogy, the high frequencies.
Why could that be relevant? Me dreaming...
From click we learned:
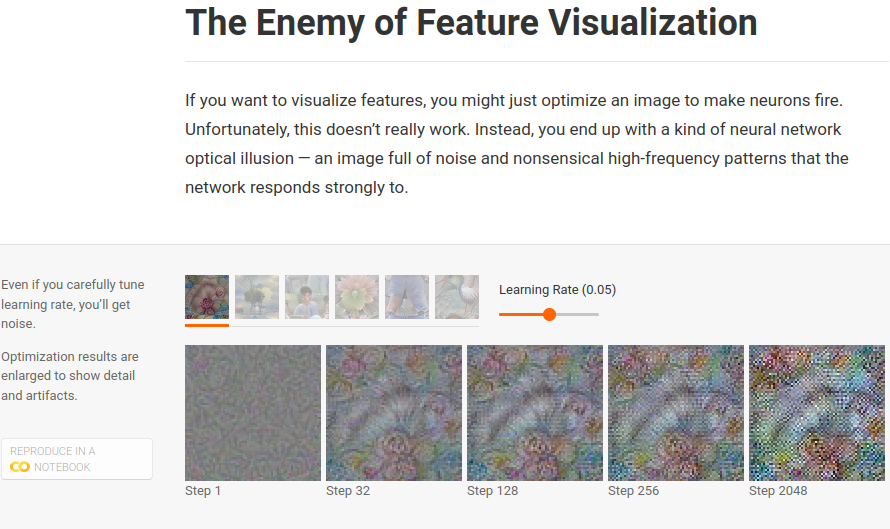
These patterns seem to be the images kind of cheating, finding ways to activate neurons that don't occur in real life. If you optimize long enough, you'll tend to see some of what the neuron genuinely detects as well, but the image is dominated by these high frequency patterns. These patterns seem to be closely related to the phenomenon of adversarial examples.
We don't fully understand why these high frequency patterns form, but an important part seems to be strided convolutions and pooling operations, which create high-frequency patterns in the gradient.
These high-frequency patterns show us that, while optimization based visualization's freedom from constraints is appealing, it's a double-edged sword. Without any constraints on images, we end up with adversarial examples. These are certainly interesting, but if we want to understand how these models work in real life, we need to somehow move past them...
In other words, one gets dominating high frequencies! Sounds familiar? Well, work in progress.