Data
- Title: Monoidal categories, representation gap and cryptography
- Authors: Mikhail Khovanov, Maithreya Sitaraman and Daniel Tubbenhauer
- Status: Trans. Amer. Math. Soc. Ser. B 11 (2024), 329-395. Last update: Mon, 12 Feb 2024 00:35:47 UTC
- ArXiv link: https://arxiv.org/abs/2201.01805
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1, Slides2, Slides3, Slides2, Slides4
Abstract
The linear decomposition attack provides a serious obstacle to direct applications of noncommutative groups and monoids in cryptography. To overcome this issue we propose to look at monoids with only big representations, in the sense made precise in the paper, and undertake a systematic study of such monoids. One of our main tools is Green's theory of cells (Green's relations). A large supply of monoids is delivered by monoidal categories. We consider simple examples of monoidal categories of diagrammatic origin, including the Temperley-Lieb, the Brauer and partition categories, and discuss lower bounds for their representations.
A few extra words
Some of
the most important cryptographic protocols in use today are based on commutative groups
and deliver a gold standard for cryptography (modulo the fear of quantum computers). On the other hand, noncommutative group-based and monoid-based
protocols seem to be less understood and in many cases admit efficient attacks.
There has been many ideas and there is an extensive literature on constructing
cryptographic protocols from noncommutative groups and monoids S (monoids generalize groups and we switch to saying monoids from now on).
As an example consider Stickel's secret key exchange. Here \(g,h\in S\) with \(gh\neq hg\) are public, party A picks \(a,a^{\prime}\in\mathbb{Z}_{\geq 0}\), party
B picks \(a,a^{\prime}\in\mathbb{Z}_{\geq 0}\), A sends \(g^{a}h^{a^{\prime}}\), B sends \(g^{b}h^{b^{\prime}}\), and the common secret is
\(g^{a}g^{b}h^{b^{\prime}}h^{a^{\prime}}=g^{b}g^{a}h^{a^{\prime}}h^{b^{\prime}}\).
Note that S can an arbitrary monoid in this protocol. The
complexity of S determines how difficult it is to find the common secret from the public data.
As shown by Myasnikov and Roman'kov (and also based on earlier work), Stickel's protocol and others in this spirit
can be successfully attacked if S admits small nontrivial representations. This is called a linear decomposition attack or
linear attack, for short.
One of the consequences of linear attacks is
that finite noncommutative groups may not be suited for
cryptographic purposes as they admit nontrivial
representations of moderate size. For a toy example, the symmetric group in \(\{1,\dots,n\}\)
has n! elements, but admits a faithful (n-1)-dimensional representation. The dimension of this
representation is logarithmic in the size of the group, and the symmetric group would be a poor
choice for various standard noncommutative group protocols.
Likewise, finite simple groups of Lie type often admit representations of (exponentially)
small dimension compared to their size. Hence, it is not surprising that some platform groups proposed in the literature are infinite.
This paper explores finite monoids (mostly coming from monoidal categories)
instead of infinite groups.
The questions we address are:
- What are (numerical) measures to determine whether a monoid can resist linear attacks?
- How to find a good supply of finite monoids for cryptographic use?
It is thus essential to find monoids that have big representation gaps or with faithful representations of big dimension only. A monoidal category delivers a supply of monoids: any object X of a monoidal category C gives rise to the family monoids \(S_{n}=\mathrm{End}_{C}(X^{\otimes n})\). In fact, monoidal categories are naturally two-dimensional structures. They often can be described via generating objects, generating morphisms and defining relations. The latter can be understood as relations on planar diagrams or networks. A natural problem is to construct examples of diagrammatically defined monoidal categories that may be useful for cryptographic purposes.
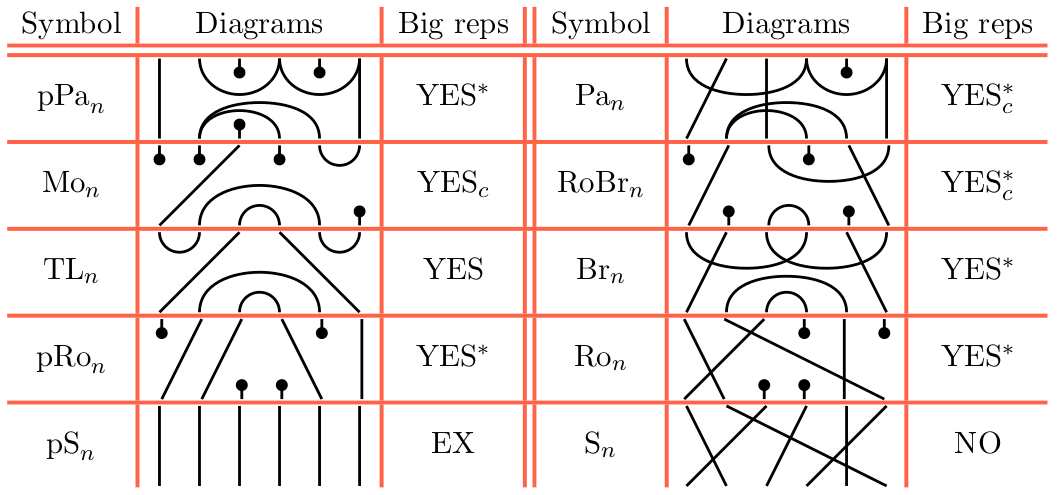
Let us take the opportunity to recall some diagrammatic monoids which we will discuss in this paper. All of these will be very familiar to the reader with background in quantum algebra, quantum topology and alike. Most of the monoids which we will use can be obtained as hom-subsets of the partition category. We will use matchings from n bottom to n top points of the following types:
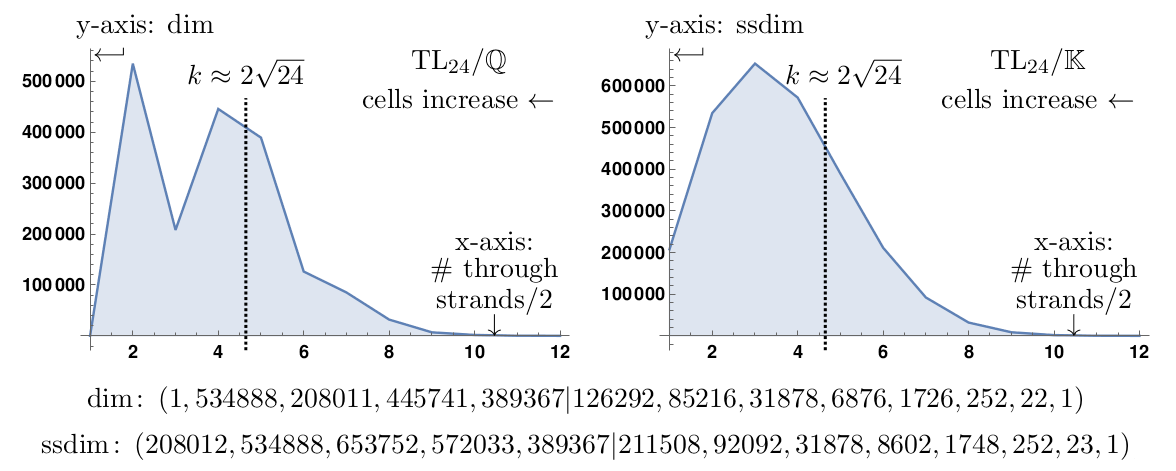
Our main tool to study monoid representations are Green's relations a.k.a. Green's theory of cells. An example how cell theory enters the paper is that a monoid can be truncated by considering a large cell submonoid. Since simple S-representations are ordered by cells, the submonoid will inherit precisely the simple S-representations for large cells. The submonoids of this form sometimes have very few small representations. Here is an example for the Temperley-Lieb monoid in 24 strands: