Data

• Title: Sandwich cellularity and a version of cell theory
• Authors: Daniel Tubbenhauer
• Status: Rocky Mountain J. Math. 54 (6), 1733-1773, (December 2024). Last update: Tue, 24 Sep 2024 21:36:03 UTC
• ArXiv link: https://arxiv.org/abs/2206.06678
• LaTex Beamer presentation: Slides1, Slides2

Abstract

We explain how the theory of sandwich cellular algebras can be seen as a version of cell theory for algebras. We apply this theory to many examples such as Hecke algebras, and various monoid and diagram algebras.

A few extra words

One of the main tools to study the representation theory of algebras is the notion of a cellular algebra due to Graham-Lehrer, and cellular algebras are nowadays ubiquitous in representation theory. Sandwich cellular algebras can be seen as a common and strict generalization of Graham-Lehrer's cellular algebras and affine cellular algebras, as well as partial generalizations of Kazhdan-Lusztig bases, monoid and diagram algebras. All of these, in a precise sense, fit under the umbrella of sandwich cellularity.
These sandwich cellular algebras are certain algebras equipped with a sandwich cell datum which in turn gives rise to the notion of cells for these algebras. Cells partition sandwich cellular algebras in the same way as Green's relations partition monoids, or more generally semigroups, and Kazhdan-Lusztig cells partition Hecke algebras. (The latter is the reason why we use the name cells.)
Cell are like ideals, and there are left cells, right cells, two-sided cells called J-cells and H-cells which are intersections of left and right cells. We think of cells as a matrix decomposition of sandwich cellular algebras:

Here we use matrix notation for the twelve H-cells in \(\mathcal{J}\) so that \(\mathcal{H}_{ij}\) is the intersection of the ith right with the jth left cell of \(\mathcal{J}\). The J-cell \(\mathcal{J}\) is then a matrix with entries from H-cells. Moreover, the left cells are column vectors and the right cells are row vectors of \(\mathcal{J}\).
The main theorem about sandwich cellular algebras is H-reduction, that reduces the classification of the simple modules of the whole algebra to the classification of the simple modules for (idempotent) H-cells.
How does this work in practice? Here is an example of how a cell structure could look like (the idempotent H-cells are marked): To classify the simple modules of this, not further specified, sandwich cellular algebra it suffices to pick one H-cell per J-cell, and classify the associated simple modules. This is a huge reduction. Here is an analogy: instead of looking at 1000 matrices of size 100x100, you pick one entry per matrix which is enough to determine the rest. This justifies the name H-reduction.
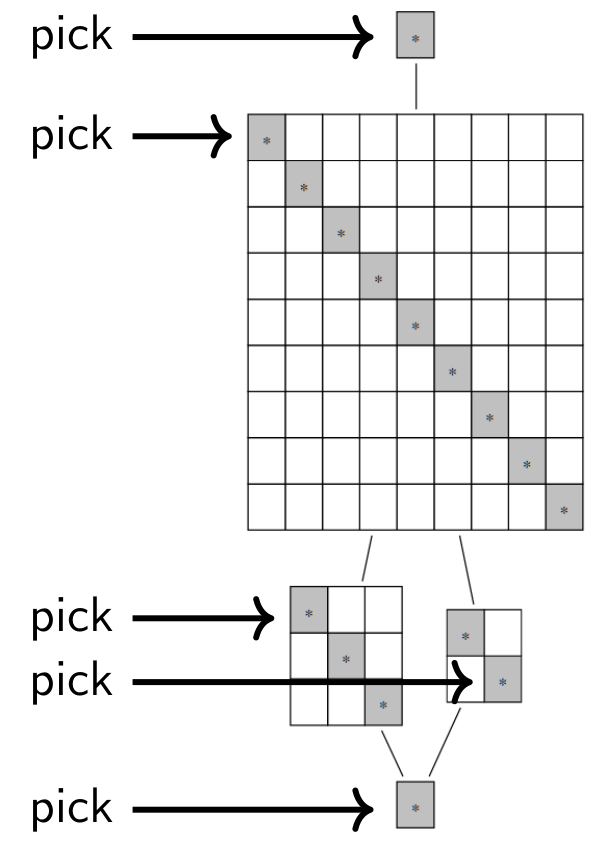
Sandwich cellular algebras are around for a long time, however, in various disguises and often implicit in the literature. They originate from at least four perspectives as mentioned above. In historical order, they appeared via the Clifford-Munn-Ponizovskiĭ theorem in monoid theory, in the study of the Brauer algebra, they are related to Kazhdan-Lusztig cells, and are generalizations of cellular algebras. In this paper we will draw connections between these different fields by taking all of these perspectives at once.