Data
- Title: Super q-Howe duality and web categories
- Authors: Daniel Tubbenhauer, Pedro Vaz and Paul Wedrich
- Status: Algebr. Geom. Topol. 17-6 (2017), 3703-3749. Last update: Tue, 21 Nov 2017 19:09:56 GMT
- ArXiv link: http://arxiv.org/abs/1504.05069
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1, Slides2, Slides3, Slides4, Slides5, Slides6
- Poster: Poster
Abstract
We use super q-Howe duality to provide diagrammatic presentations of an idempotented form of the Hecke algebra and of categories of \(\mathfrak{gl}_n\)-modules (and more generally \(\mathfrak{gl}_{N|M}\)-modules) whose objects are tensor generated by exterior and symmetric powers of the vector representations. As an application, we give a representation theoretic explanation and a diagrammatic version of a known symmetry of colored HOMFLY-PT polynomials.
A few extra words
We discuss a machine that “takes dualities
and produces diagrammatic presentations of the related
representation theoretical categories”.
Specifically, we feed the machine
with super q-Howe duality
between the superalgebra \(\textbf{U}_q(\mathfrak{gl}(m|n))\) and \(\textbf{U}_q(\mathfrak{gl}_N)\).
We construct diagrammatic presentations of an idempotented form of the
Iwahori-Hecke algebra as well as of categories of \(\textbf{U}_q(\mathfrak{gl}_N)\)-modules
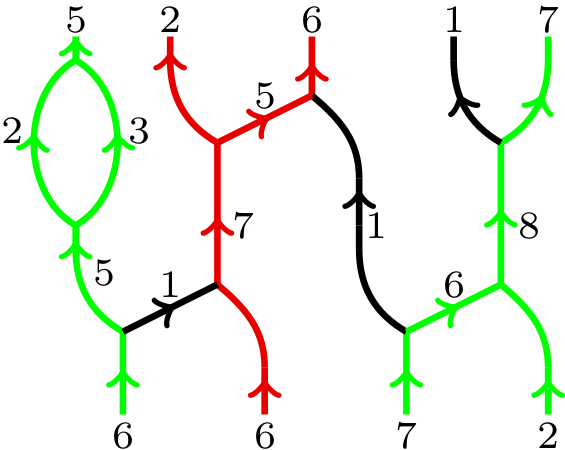
by using the “green-red” web
categories \(\infty\text{-}\!\textbf{Web}_{\mathrm{gr}}\) and \(N\text{-}\!\textbf{Web}_{\mathrm{gr}}\).
Morphisms in these \(\mathbb{C}_q\)-linear categories
are combinations of planar, upwards oriented,
trivalent graphs with edges labeled by positive integers
and colored black, green or red modulo local relations.
An example of a green-red web is: