Data
- Title: Symmetric webs, Jones-Wenzl recursions and q-Howe duality
- Authors: David E.V. Rose and Daniel Tubbenhauer
- Status: Int. Math. Res. Not. (IMRN), 2016-17 (2016), 5249-5290. Last update: Sun, 9 Sep 2018 19:07:14 GMT
- ArXiv link: http://arxiv.org/abs/1501.00915
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1, Slides2, Slides3, Slides4, Slides5, Slides6, Slides7, Slides8
- Poster: Poster
Abstract
We define and study the category of symmetric \(\mathfrak{sl}_2\)-webs. This category is a combinatorial description of the category of all finite dimensional quantum \(\mathfrak{sl}_2\)-modules. Explicitly, we show that (the additive closure of) the symmetric \(\mathfrak{sl}_2\)-spider is (braided monoidally) equivalent to the latter. Our main tool is a quantum version of symmetric Howe duality. As a corollary of our construction, we provide new insight into Jones-Wenzl projectors and the colored Jones polynomials.
A few extra words
A classical result of Rumer, Teller and Weyl,
modernly interpreted, states that the so-called Temperley-Lieb category \(\mathcal{TL}\) describes
the full subcategory of quantum \(\mathfrak{sl}_2\)-modules
generated by tensor products of the 2-dimensional vector representation V
of quantum \(\mathfrak{sl}_2\).
By Karoubi completion, we get the whole category of finite dimensional \(\mathfrak{sl}_2\)-modules. Thus, it is a striking question if one can give a
diagrammatic description of \(\mathbf{KAR}(\mathcal{TL})\) as well.
We provide a new
diagrammatic description of the entire category of
finite dimensional quantum \(\mathfrak{sl}_2\)-modules.
To this end, we introduced our new description of the representation
theory of quantum \(\mathfrak{sl}_2\), the category of
symmetric \(\mathfrak{sl}_2\)-webs akin
to the category of “usual” \(\mathfrak{sl}_n\)-webs studied by many people (recall that
these “usual” \(\mathfrak{sl}_n\)-webs give a diagrammatic presentation of the full subcategory of all finite dimensional
\(\mathfrak{sl}_n\)-modules whose objects are
finite tensor products of the fundamental
\(\mathfrak{sl}_n\)-representations.
Our main tool is the usage of symmetric q-Howe duality.
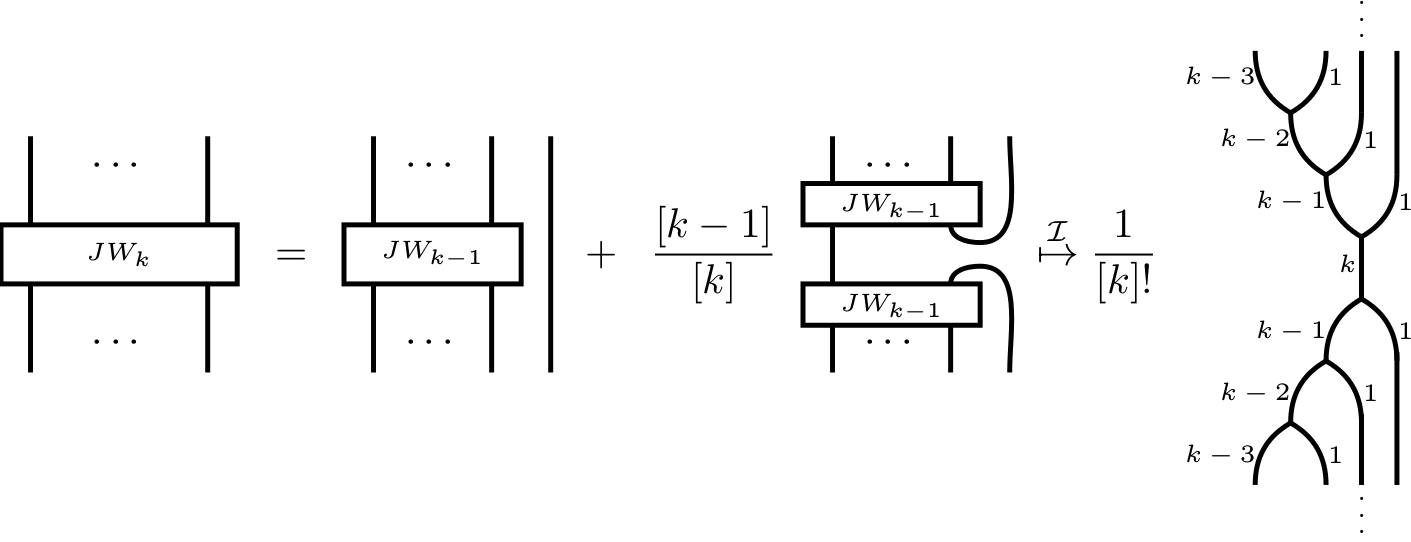
In particular, the Jones-Wenzl projectors are included in our picture, but without any recursive formula. Namely, they are directly given as below.
Another corollary of our construction is a “MOY-calculus” for colored Jones polynomials.